[论文笔记] A Survey of Model Compression and Acceleration

发表于 2020-08-28

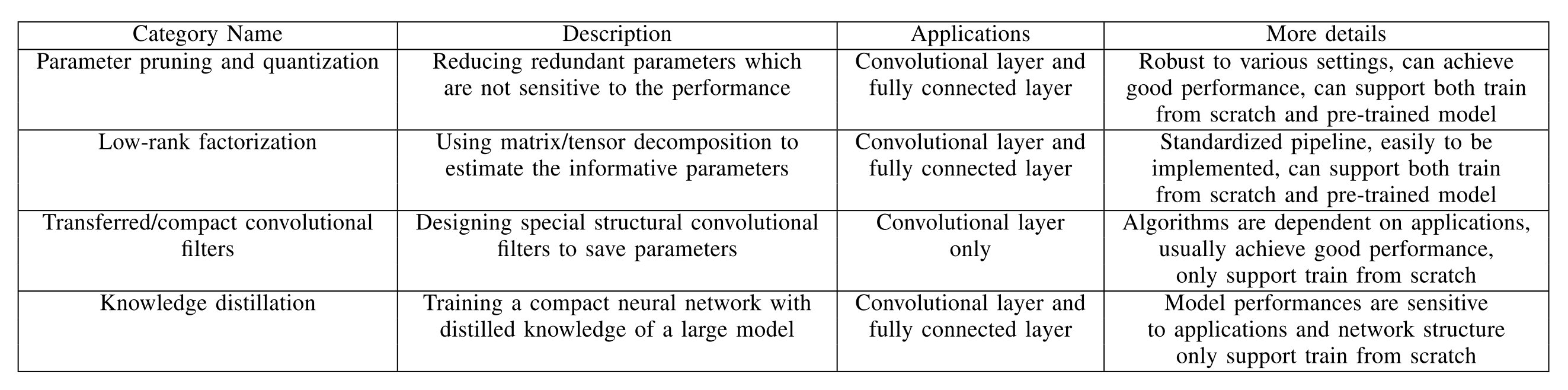
这是一篇模型压缩领域的综述，主要从参数剪枝和量化（Parameter pruning and quantization），低秩分解（Low-rank factorization），转移/紧致卷积滤波器（Transferred/compact convolutional filters）和知识蒸馏（Knowledge distillation）四个方面来对于已有的模型压缩方法进行综述。这篇文章发表的时间点为2017年，可能对于较新的成果涉及并不是那么广泛，但是对于模型压缩加速领域的一个初步了解而言感觉还是可以的。

四个方向的总体概览如下所示：

参数剪枝和量化（Parameter pruning and quantization）

量化与二值化（Quantization and Binarization）

网络量化是通过用来表示权重的bits数目来将原网络进行压缩的，比如可以采用16-bit浮点或者是8-bit整数来表示权重，极限情况下可以采用1-bit的二进制权重神经网络。

同时也有一种方法是通过权重共享来实现模型的压缩，可以认为是通过Hash方法将所有近似的权重对应于一个Hash值，即使得相同的权重只被存放一次。这里通过哈夫曼编码来减少存放索引所需要的空间，从而可以通过索引去读取对应的内容。

流程如下所示：

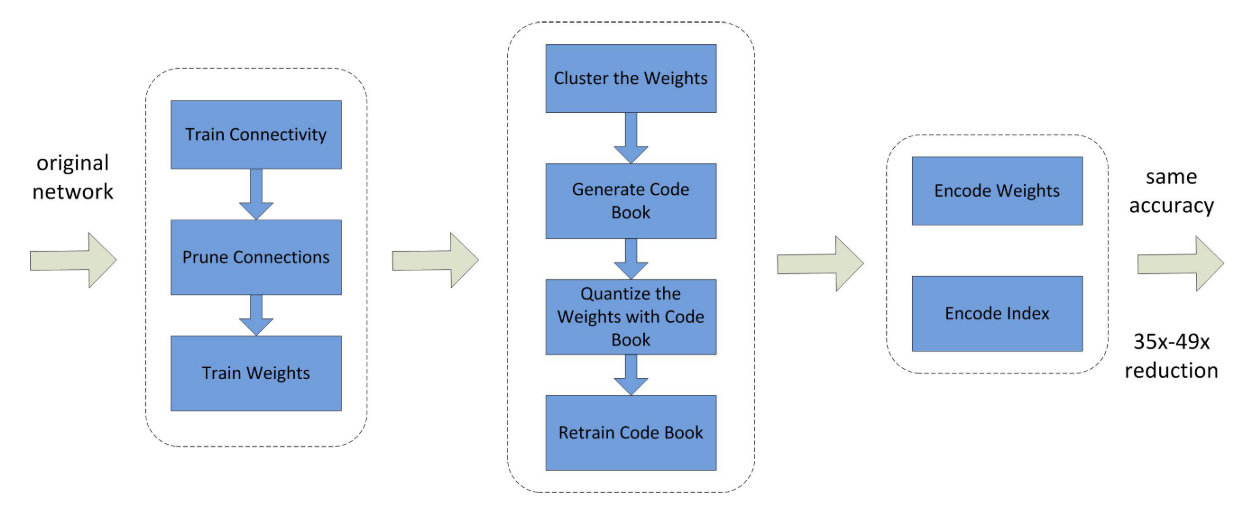
他实际上在利用Code Book量化之后会对共享的权重进行重训，来得到更好的效果。最后得到的就是权重的Code Book，每个权重存放的是对应的索引而不是权值。

（好奇.jpg，离散值的梯度反传等等怎么搞？找到了个知乎链接，有空看看，估摸着是不一定会看了)

缺点：

二进制网络的精度降低非常严重。
当前的二进制方案基于简单的矩阵估计，忽略了二进制在精度损失方面的效果。

网络剪枝（Network Purning）

网络剪枝和共享已经被用于减少网络复杂性和处理过拟合任务。一个早些的剪枝方法是有偏的权重衰减。最优脑损害(The Optimal Brain Damage)和最优脑外科医生(the Optimal Brain Surgeon)方法基于损失函数Hessian矩阵来减少连接层的参数，这些工作期望能够比基于大小的剪枝方法（比如权重衰减）有更高的准确率。

网络剪枝的最近一个方向是剪枝掉预训练模型当中的冗余权重，通过data-free的方式来去除掉冗余的神经元和连接。

同时也有一个方向是训练带有稀疏性约束的CNN网络。在最优化问题当中，稀疏性约束通常就是 $l_0$ 和 $l_1$ 正则化。

缺点：

利用 $l_1$ 或者是 $l_2$ 正则化通常需要更多的迭代来收敛
所有的剪枝条件都一定程度上需要人工来设置网络层的敏感性
网络剪枝通常能够降低模型大小但是没有办法提升效率

构造结构化矩阵（Designing Structural Matrix）

结构化矩阵的方式从我的理解来看，实际上就是通过更少的参数来表示全连接层的那个大矩阵，从而降低需要的参数量。由于有的结构化方法可以通过特性进行高效的矩阵-向量乘法，所以不仅可以降低内存的消耗，同时可以加速模型的训练和推断。

（好奇.jpg x 2，卷积实际上应该也是一种结构化矩阵，这玩意能不能在受限情况下进行搜索？）

一种方法就是通过循环投影（circulant projections），通过向量 $\mathbf{r}=(r_0,r_1,\ldots,r_{d-1})$ ，一个循环矩阵 $\mathbf{R}\in \mathbf{R}^{d\times d}$ 可以如下定义：

$\mathbf{R}=\text{circ}(\mathbf{r}):=\left[\begin{array}{ccccc} r_{0} & r_{d-1} & \ldots & r_{2} & r_{1} \\ r_{1} & r_{0} & r_{d-1} & & r_{2} \\ \vdots & r_{1} & r_{0} & \ddots & \vdots \\ r_{d-2} & & \ddots & \ddots & r_{d-1} \\ r_{d-1} & r_{d-2} & \ldots & r_{1} & r_{0} \end{array}\right]$

这使得内存消耗从 $O(d^2)$ 变成了 $O(d)$ ，同时循环矩阵也可以利用快速傅立叶变换（FFT）来加速计算过程。提供一个 $d$ 维的向量，通过上述矩阵的计算时间复杂度为 $O(d\log d)$ 。

缺点：

结构化约束会使得模型有偏，损害模型的性能（我的角度来看就是做了不该做的假设）
很难找到合适的结构化矩阵，当前也缺乏理论指导

低秩分解（Low-rank factorization）

卷积操作占据了深度CNNs模型中的最大计算篇幅，因此减少卷积层能够提升压缩率同时也能加快运算速度。

对于卷积核，它可以被认为一个4D张量。基于张量分解的想法驱使我们本能的认为4D张量的冗余性去除会有一个显著提升，这是一个特殊的方式去移除冗余性。注意到全连接层，它能够被视为一个2D矩阵并且低秩也能有所帮助。

很长时间以来，人们使用低秩滤波器去加速卷积，例如，高维DCT（discrete cosine transform,）和小波系统（wavelet systems）各自使用张量积去构造从一维DCT和小波。

低秩估计是逐层而做的。一层的参数在低质估计后固定下来，而上面的层是微调基于一个重构误差准则。这些是典型的用于压缩2D卷积滤波器的低秩估计方法。根据这个方向，Canonical Polyadic(CP)分解是一个用于核张量的方法。人们使用非线性的最小二乘去计算CP分解。然而，找到最好的低秩估计在CP分解中式一个病态问题，并且最好的 $rank-K$ （K是秩的值）估计可能是不存在的。

正如前面所提，全连接层可以看成是2D矩阵，因此上述的方法（指低秩估计的方法）也能够应用到这儿（指全连接层的分解）。也有工作应用截断奇异值分解去分解全连接层用于设计紧凑的多任务深度学习框架。

缺点：

低秩方法涉及到计算代价昂贵的分解操作，执行起来并不容易。
由于不同层有着不同的信息，当前的低秩估计方法是逐层的，因此不能执行全局的参数压缩。
比较原始模型，分解需要额外的再训练去实现收敛。

转移/紧致卷积滤波器（Transferred/compact convolutional filters）

CNNs 是参数有效的对于转换的不变性，对于输入图片表示的不变性，而这对于训练深度模型而不导致过拟合是重要的。尽管目前还缺失强理论证明，但是大量的经验事实支持平移不变性和权重共享对于好的预测性能是重要的。使用转移卷积滤波器去压缩CNN模型的想法受到研究工作启发，它引入了等价理论。让 $x$ 是一个输入， $\Phi(\cdot)$ 是一个网络层和 $\mathcal{T}(\cdot)$ 是一个转换矩阵。等价性的概念如下所定义：

$\mathcal{T}^\prime(\Phi(x)) = \Phi(\mathcal{T}x)$

表明转换了 $\mathcal{T}(\cdot)$ 的输入 $x$ 然后传递它到层次 $\Phi(\cdot)$ 的网络（即得到 $\mathcal{T}x$ 后再用网络作用）应该有同样的结果在第一次用网络映射 $x$ 然后再转换表示（即先得到 $\Phi(x)$ ，再用 $\mathcal{T}$ 作用)。注意： $\mathcal{T}^\prime(\cdot)$ 和 $\mathcal{T}(\cdot)$ 不是必须相同的。根据这个理论，应用转换层或者滤波器 $\Phi(\cdot)$ 去压缩整个网络模型是合理的。从经验观察，深度CNNs同样受益于使用大的卷积滤波器通过应用确定的转换 $\mathcal{T}(\cdot)$ 到一个小的基础偏置滤波器的集合，由于它扮演了一个模型的正则化。

在这个方向，有许多最近的研究工作去建立一个由基础滤波集合构建的卷积层。（就是从不同的角度定义函数 $\mathcal{T}(\cdot)$ ）

缺点：

这些方法能够对于宽度（扁平）的框架（比如VGGNet）能够实现竞争性的性能，但是对于深度的网络（比如GoogleNet，ResNet）效果就不是很好。
指导学习的转移假设条件有时太强了，这使得结构对于某些情形是不稳定的。

知识蒸馏（Knowledge Distillation）

知识蒸馏的基本想法就是将深度大模型中蒸馏知识到一个浅层的网络当中。压缩的网络会尝试学习深层复杂网络的这样一个映射。通常的方法就是通过学习softmax之后的分布来讲大模型的知识蒸馏到小模型当中。当然也有一些工作来尝试学习高层隐层当中的表征，或者是feature maps来进行知识蒸馏，以获得相对于最终的分布更多的信息。通常而言大模型和压缩模型的容量结构相差比较大，假设其中间结果有着相似效果是一个过强的约束。

缺点：

知识蒸馏的方法可以显著降低运算量，但是只能够被用在softmax loss的任务上。
只能够从头开始训练，不能够从已有的模型权重当中进行抽取。
效果相对于其他方法而言也并不够好。

评测指标与数据集

数据集

数据集主要为主流的图像相关任务数据集，对应的Baseline模型为主流的CV经典模型，如ResNet，VGG nets等。

评测指标

记 $M$ 为模型， $a$ 为模型所含有的参数数量， $s$ 为模型的运行时间，大部分工作是采用的平均每epoch的训练时间，但是实际上测试时间也是可以的。利用 $M^*$ 的星号上标来表示压缩后模型的对应指标，通常采用的评价指标有以下几种：

压缩比率（compression rate）

$\alpha(M, M^*) = \frac{a}{a^*}$
索引空间节省量（index space saving）

$\beta(M, M^*) = \frac{a - a^*}{a^*}$
加速比率（speedup rate）

$\delta(M,M^*) = \frac{s}{s^*}$

通常而言压缩比和加速比是高度相关的，因为越小的模型通常跑的越快。事实上在不同的任务当中这可能和不同的层类型是相关的。大多是任务的运算主要集中在全连接层，但是对图像分类任务而言，绝大多数的运算主要集中在卷积层，因为一开始的图像面积比较大，卷积层运算非常耗时间。所以具体的压缩和加速方法需要对应于不同的应用着重关注不同类型的网络层。

[论文笔记] (CGD) Combination of Multiple Global Descriptors for Image Retrieval

发表于 2020-08-13

Introduction

基于深度学习的图像检索任务通常是利用CNN网络进行特征提取，将图片转化为一个向量，然后通过之后通过向量来进行相关图片的检索。那么怎么利用CNN提取出一个有效的全局描述符实际上就成为了一个非常关键的步骤。

这篇论文提出了一种不需要训练多个网络再融合就能够将多个全局描述符进行融合的方法。

提出了CGD网络（combination of multiple global descriptors），可以融合多种全局描述符并且进行端对端的训练，同时在backbone，loss等方面都有着良好的拓展性。
通过量化实验说明了融合多种全局描述符比单个有着更好的表现。
在多个图像检索数据集上都达到了sota水平。

CGD模型的总体结构如下：

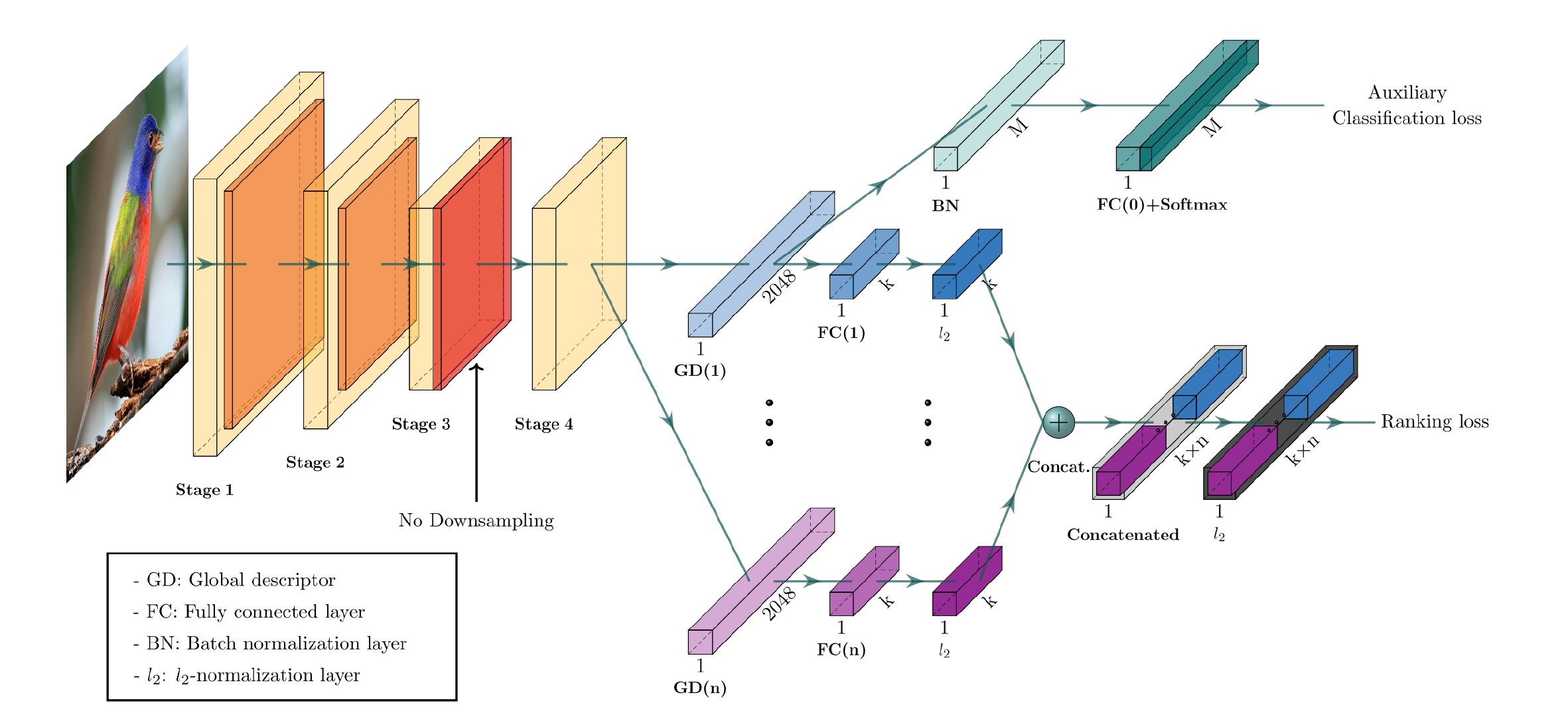
可以看到它主要由一个CNN backbone和两个模块组成。下面的主模块是主要的用于学习图像表示的模块，他组合了多个全局描述符，利用ranking loss进行优化，上方是一个用来对CNN backbone进行fine-tune的辅助模块，利用classification loss进行优化。最终的loss为以上两个loss的总和，这样就可以直接将整个网络进行一个端到端的训练了。

Main Module

这边是把最后一层卷积层的结果作为输入，是一个 $C\times H\times W$ 的三维张量，记作 $\mathcal{X}$ ，通过一个池化操作可以转化为一个向量，池化操作可以写成如下一个统一形式：

$f_c = \left(\frac{1}{|\mathcal{X}_c|} \sum_{x \in \mathcal{X}_c}x^{p_c}\right)^{\frac{1}{p_c}}$

其中下标c表示的是c通道的结果，三种全局描述符的表示对应如下：

SPoC： $p_c=1$
MAC： $p_c\rightarrow \infty$
GeM：默认为 $p_c=3$ ，可以手动设置为任意值，或者当作可训练的参数

如总框架中所示的，在经过一个池化操作之后，需要需要通过一个全连接层降维再进行L2正则化，得到最终的输出特征 $\Phi^{(a_i)}$

$\Phi^{(a_i)} = \frac{W^{(i)}\cdot f^{(a_i)}}{|| W^{(i)}\cdot f^{(a_i)}||_2},\qquad a_i\in \{s,m,g\}$

其中 $i$ 表示第 $i$ 个分支， $a_i$ 的三种取值对应上述提到的三种池化操作，最终的特征向量是一个组合描述符，将多个分支的结果进行拼接再进行L2正则化：

$\psi_{C G D}=\frac{\Phi^{\left(a_{1}\right)} \oplus \ldots \oplus \Phi^{\left(a_{i}\right)} \oplus \ldots \oplus \Phi^{\left(a_{n}\right)}}{\left\|\Phi^{\left(a_{1}\right)} \oplus \ldots \oplus \Phi^{\left(a_{i}\right)} \oplus \ldots \oplus \Phi^{\left(a_{n}\right)}\right\|_{2}}$

这样就在一个CNN backbone的基础上，只通过了很少的参数添加就获得了组合描述符的效果。

Auxiliary Module

辅助模块通过第一个全局描述符来对接前面的CNN backbone进行fine-tune。通过一个分类任务来帮助最大化图片的组间距离，同时使得模型的训练速度更快。这里采用Temperature scaling和label smoothing的方法来帮助训练，最终的softmax loss定义如下：

$L_{Softmax}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{\exp \left(\left(W_{y_{i}}^{T} f_{i}+b_{y_{i}}\right) / \tau\right)}{\sum_{j=1}^{M} \exp \left(\left(W_{j}^{T} f_{i}+b_{j}\right) / \tau\right)}$

$\tau$ 是用来缩放的温度，越低实际上扩大了不同类之间的差距，增强学习的效果。

More Discussion

Configuratons

CGD完成的实际上是多种描述符的组合，在这里一共有3种池化操作。如果有多个描述符的话，第一个的结果要做用到下游的分类任务，所以相对于其他有所区别。于是这里一共有12种不同的描述符：

$S,M,G,SM,MS,SG,GS,MG,GM,SMG,MSG,GSM$

选择的方法就是首先用单个描述符来进行测试，跑3次实验，之后选择其中最优的和次优的进行组合。

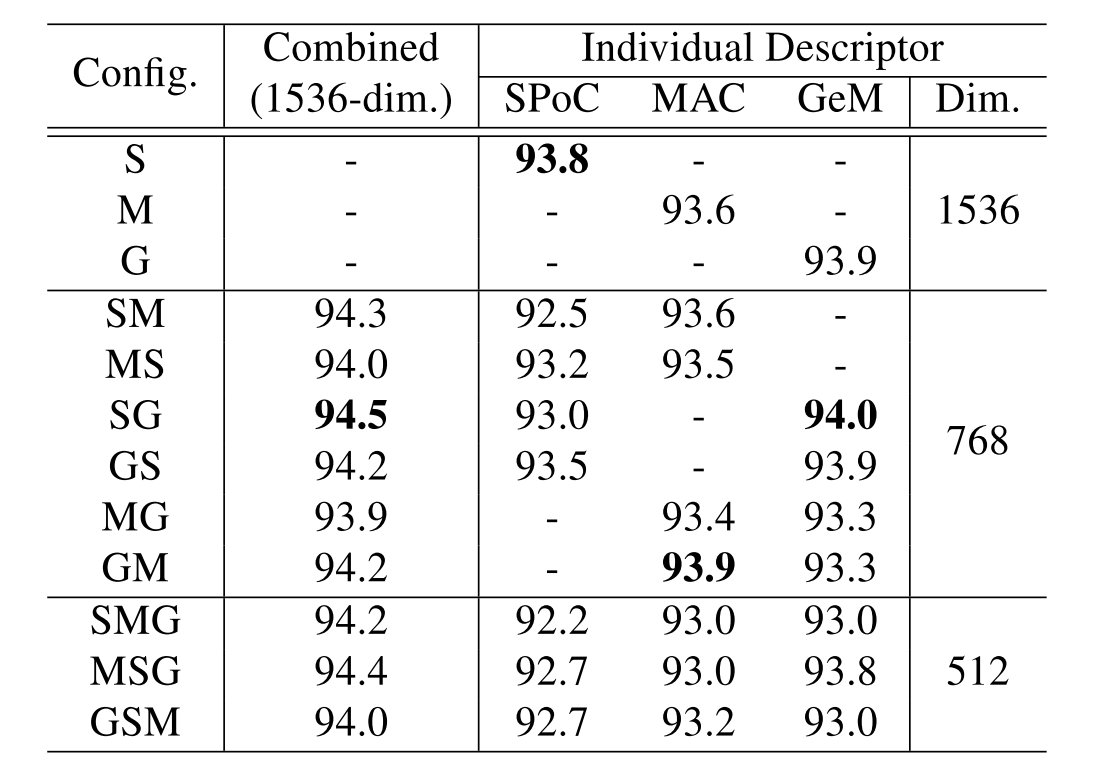
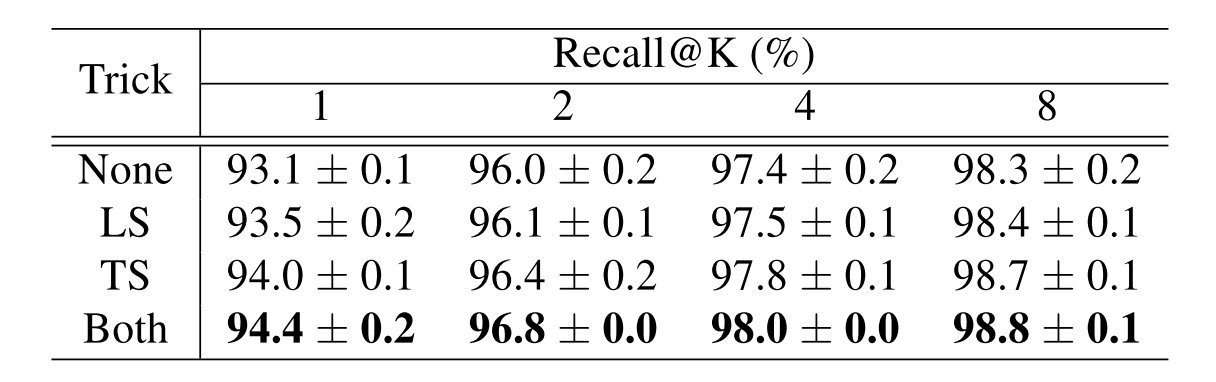
Label Smoothing and Temperature Scaling

在实验当中得到的结果是，两种trick都采用在ResNet-50 backbone上有着一定程度的提升：

Position of Combination

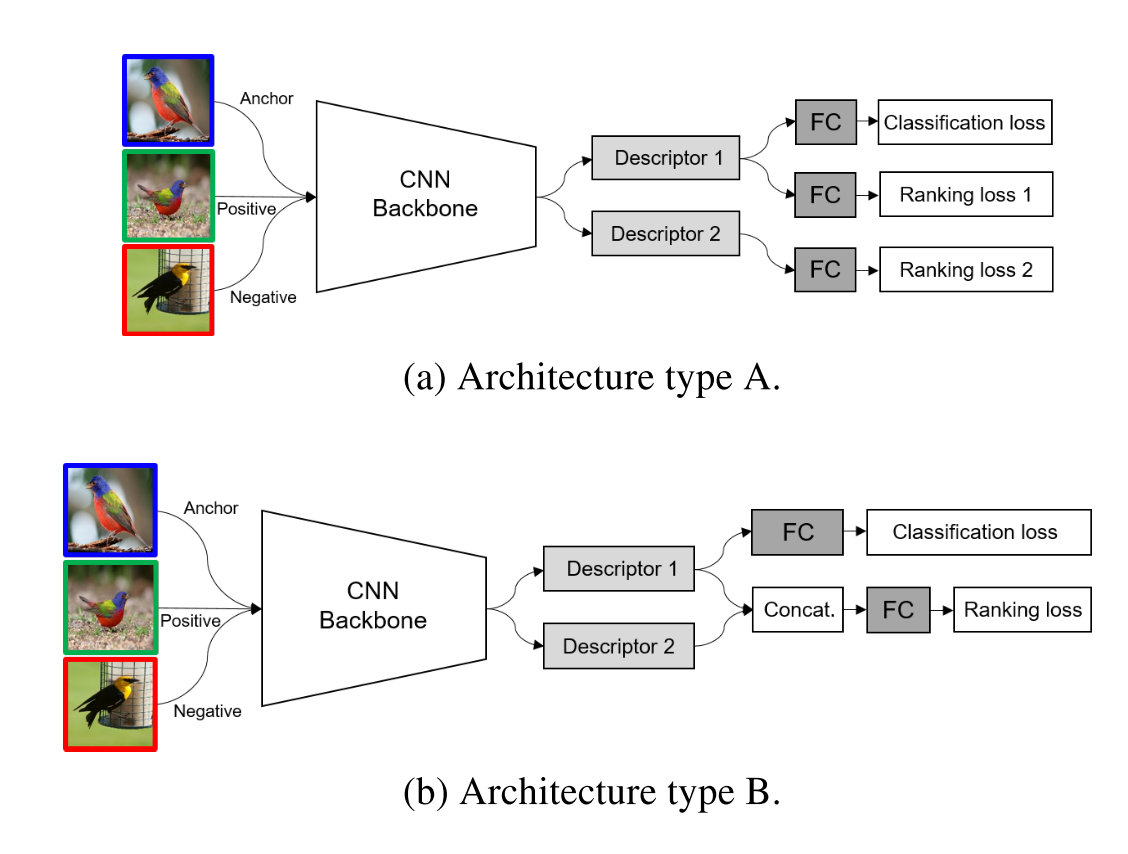
对于在什么位置进行多种全局描述符的融合也进行了试验，两种方法如下所示：

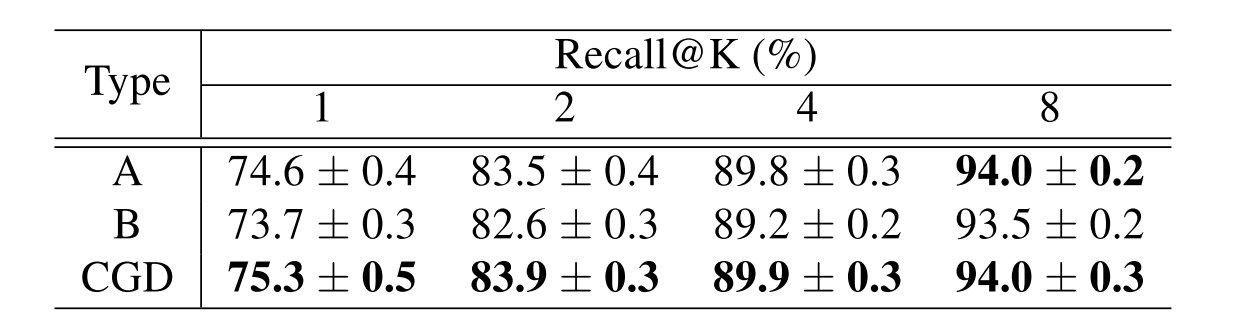
得到的结果如下，可以发现CGD模型的框架在总体情况下是更优的：

Method of Combination

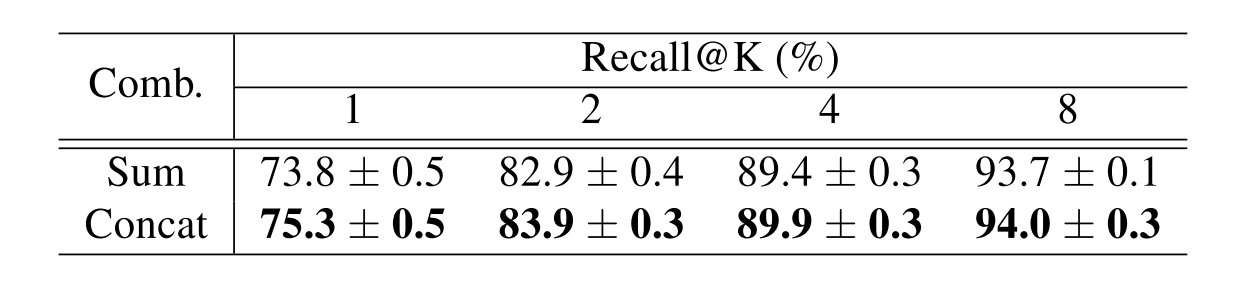
对于组合的方法考虑了直接进行求和和进行拼接两种方法，可以发现拼接可以保存更多的特性和多样性，能够取得更好的最终结果：

Implementation Details

实现的具体参数列在下方：

transform:
  training phase:
    resize: 252 x 252
    random crop: 224 x 224
    randomly flipped to horizontal
  inference phase:
    resize: 224 x 224
  	
optimizer:
  Adam:
    learning rate: 1e-4
    
batch size: 128
margin for triplet loss: 0.1
temperature: 0.5
label smoothing: 0.1

Code

提供一个基于PyTorch的实现如下：

import torch
import torch.nn as nn
import torch.nn.functional as F

class Identify(nn.Module):
    def __init__(self):
        super().__init__()
        
    def forward(self, x):
        return x

class L2Normalization(nn.Module):
    def __init__(self, p=2, dim=-1):
        super().__init__()
        self.p = p
        self.dim = dim
        
    def forward(self, x):
        out = F.normalize(x, p=2, dim=-1)
        return out

class GlobalDescriptor(nn.Module):
    def __init__(self, pooling_type, trainable=False):
        super().__init__()
        if trainable:
            self.p = nn.Parameter(torch.tensor([3.]))
        else:
            self.p = 3
        if pooling_type == 's':
            self.method = nn.AdaptiveAvgPool2d(1)
        elif pooling_type == 'm':
            self.method = nn.AdaptiveMaxPool2d(1)
        else:
            def GeM(x):
                mean_value = torch.mean(torch.pow(x, self.p), dim=[-1, -2], keepdim=True)
                out = torch.sign(mean_value) * torch.pow(torch.abs(mean_value), 1 / self.p)
                return out
            self.method = GeM
        self.flatten = nn.Flatten()
    def forward(self, x):
        out = self.method(x)
        out = self.flatten(out)
        return out

class CGDModel(nn.Module):
    def __init__(self, gd_config, feature_dim=1536):
        super().__init__()
        assert feature_dim % len(gd_config) == 0
        self.pretrained_model = torch.hub.load('zhanghang1989/ResNeSt', 'resnest101', pretrained=True)
        self.pretrained_model.layer4[0].avd_layer = Identify()
        self.pretrained_model.layer4[0].downsample[0] = Identify()
        self.backbone = nn.Sequential(
            self.pretrained_model.conv1,
            self.pretrained_model.bn1,
            self.pretrained_model.relu,
            self.pretrained_model.maxpool,
            self.pretrained_model.layer1,
            self.pretrained_model.layer2,
            self.pretrained_model.layer3,
            self.pretrained_model.layer4,
        )
        
        self.n = len(gd_config)
        self.k = feature_dim // self.n
        
        self.gds = nn.ModuleList([GlobalDescriptor(i) for i in gd_config])
        self.bn = nn.BatchNorm1d(2048)
        self.fc0 = nn.Linear(2048, CLASS_NUM)
        self.fcs = nn.ModuleList([nn.Sequential(nn.Linear(2048, self.k), L2Normalization()) for i in range(self.n)])
        self.l2norm = L2Normalization()
    
    def forward(self, x):
        shared_feature = self.backbone(x)
        descriptors = []
        for i, (gd, fc) in enumerate(zip(self.gds, self.fcs)):
            feature = gd(shared_feature)
            if i == 0:
                logit = self.bn(feature)
                logit = self.fc0(logit)
            feature = fc(feature)
            descriptors.append(feature)
        global_descriptor = torch.cat(descriptors, dim=-1)
        global_descriptor = self.l2norm(global_descriptor)
        return global_descriptor, logit

Jupyter Lab 虚拟环境配置

发表于 2020-08-11

对于Anaconda的使用往往通过Jupyter Notebook或者是Jupyter Lab来进行的，可以通过以cell为单位交互式的运行，能够极大的提升效率。但是当面对与多个虚拟环境的时候，需要在Jupyter Lab当中进行虚拟环境的配置。

进行虚拟环境的管理需要安装nb_conda包：

1	conda install nb_conda

安装完成之后可以在创建notebook时，或者在执行中通过kernel选项来进行虚拟环境的选择。

当创建了新的conda虚拟环境的时候，可以在新环境上面安装ipykernel，之后重启Jupyter Lab即可，安装指令如下：

1	conda install -n env_name ipykernel

2020北大叉院/信科保研经历分享

发表于 2020-07-30

2020年由于新冠疫情影响，出国人数减少，再加上近年来硕士名额转成博士名额的趋势，使得保硕士难度会比往年更高，当然如果这个趋势不变，可以预见难度只会越来越高。

比较幸运的是今年还是拿到了想要的offer成功上岸，这里将北大叉院和信科保研的相关经历记录，希望能够帮助之后准备保研面试的同学。不过今年由于疫情，很多流程都较往年有所更改，估计参考价值有限。

个人条件

入学在工学院，大一平转信科，GPA前10%，辅修北大国发院经济学双学位。

大一大二都拿了奖学金和奖励，无国奖，无论文，无企业实习经历。

从个人角度来看，自身并不想走学术这条路，排序为：

硕士 > 工作 > 博士

大三在AIIC（北京大学人工智能创新中心）有一年实习经历，计划为保AIIC的学硕，同时在比较早就报了叉院项目希望能够保底。

北大叉院

流程

今年由于疫情取消了机考，形式为笔试+面试。

笔试

笔试一共有3道题目，题目主要考察基础的编程与算法相关的内容，难度较低。可以参考数据结构或是算法分析的课程内容来进行复习。

面试

面试形式为多对一，多为面试老师，一位学生，流程大致如下：

英文自我介绍，时长大约两分钟
简历相关问题（问了我简历上的一个项目大概是怎么做的）
个人意向相关
- 读研or读博
- 学术导向还是产业导向（这边老师问我为什么经历和陈述都更像创业导向，我直接表明自己不是很想做学术，之后就开始问数学问题了）
数学基础问题（就我与其他人的交流好像其他人没怎么被问到）
1. 神经网络：ResNet结构
2. 高等代数：特征值特征向量，SVD分解，正交矩阵和相关性质
3. 计算方法：牛顿法
4. 概率统计：一元和多元正态分布公式，贝叶斯公式和解释

结果

当表明自己不想做学术的时候感觉就应该凉了，但是可能是因为数学问题都答得没什么问题，所以最后给了个Waiting List，在七月底补录为优秀营员，我直接拒绝了offer。

推荐准备北大叉院的保研面试还是以学术导向为主，最好能够展现出自己想在学术领域继续研究的意图。

北大信科

流程

由于疫情影响取消了机考之后，信科只有一轮面试，具体形式内容应当是各个系所自己组织，我报的是北大AIIC的人工智能产业创新学硕项目。

面试

形式同样为多对一，多位面试老师，一位学生。由于之前已经在中心实习一年加上老师对于实习生已经有过了一轮面试，整体的面试氛围偏向轻松。

自我介绍
简历相关问题
个人经历问题

结果

没有官方邮件通知，第二周周中直接公示名单，成功上岸。

[论文笔记] (SPP) Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition

发表于 2020-07-21

简介

首先要解决的就是为什么需要空间金字塔池化（SPP）这个问题，它到底为了什么而出现。

对于以往的神经网络结构大部分所需要的都是固定的网络大小输入，但是现实中很多图片数据并不是固定大小的输入。以往的方法往往是通过裁剪（Crop）和扭曲（Warp），但是前者会导致信息的丢失，后者可能会导致图片的失真，都会使得数据分布发生一定变化。

SPP解决的就是图片大小不同的问题，使得输入可以是任意宽和高的图片。

Spatial Pyramid Pooling Layer

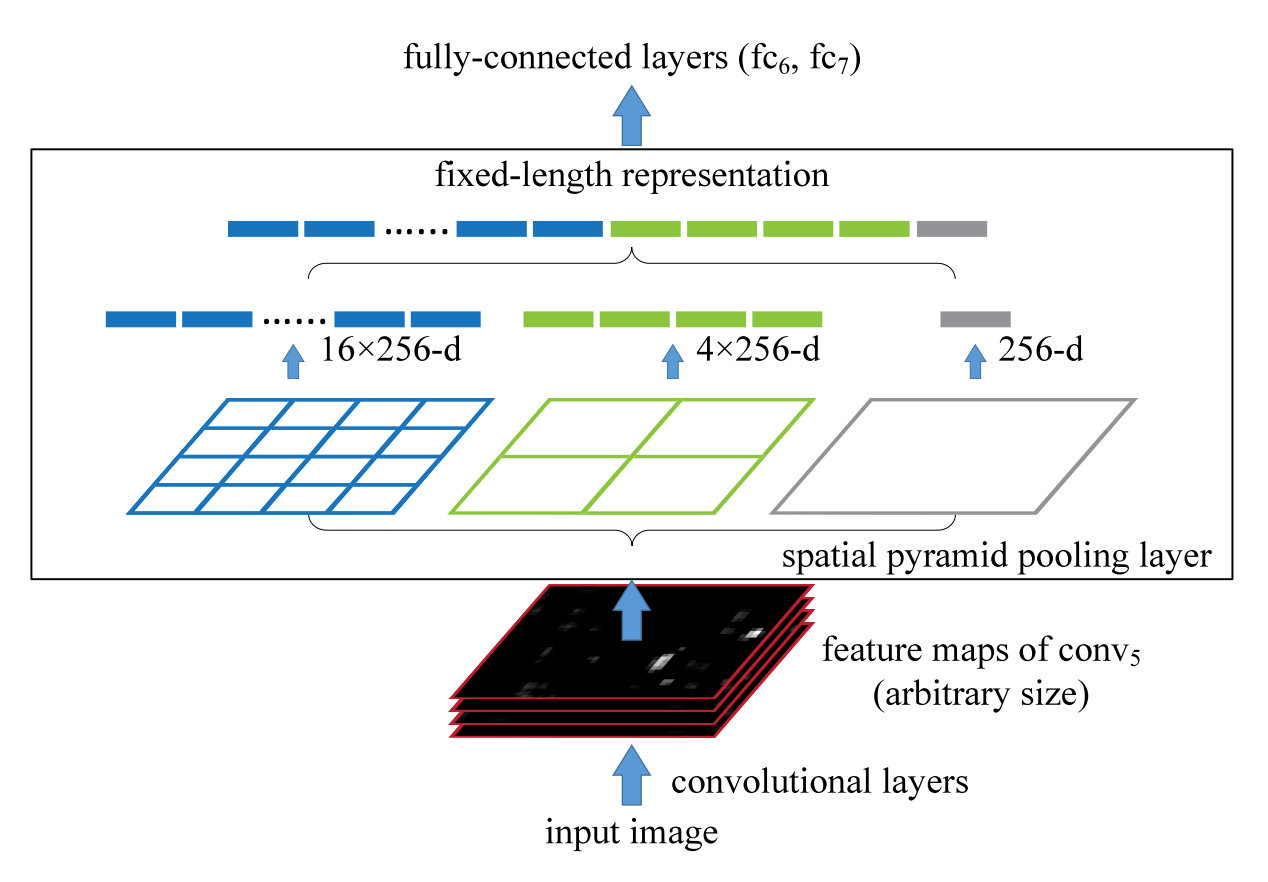
如上图所示的SPP-Net 中有若干个并行的池化层，将卷积层的结果 $w\times h\times d$ 池化成 $[1\times 1],[2\times 2],[4\times4],\cdots$ 的一层层结果，再将其所有结果进行拼接之后与 FC 层相连。

由于只有最后的FC层对于输入的大小是存在硬性要求的，当输入为任意大小的图片时，我们可以随意进行卷积、池化。在过FC 层之前，通过 SPP 层，将图片抽象出固定大小的特征（即多尺度特征下的固定特征向量抽取）。

好处有以下几点：

SPP可以针对于不同的input size输出固定长度的向量，这是原本的滑动窗口池化做不到的
SPP用了多层级的空间信息，而滑动窗口池化操作使用的窗口大小是单一的
由于输入的大小是可以变化的，所以SPP可以提取到不同尺度上信息

Training

Single-size Training

单输入size大小的训练方法同普通的训练相同，这里所需要的就是设置好对应的pooling层的stride和window size，以便于之后的SPP层可以输出正确的结果。事实上，这里为了探究single-size的训练主要是为了来测试金字塔池化的行为是否符合预期。

Multi-size Training

为了防止切换数据带来的overhead过高，这里假设有两种size的输入图片，每一种size训练一个epoch之后切换到另一种。事实上发现采用多尺度的图片，收敛速率和单尺度图片是相似的，并没有带来收敛速率上的损失。

以上两种方法都是只针对训练阶段的，在测试阶段，可以直接将任何尺寸的图片输入到SPP-net当中。

代码实现

基于PyTorch框架的实现如下，在github上看了几个实现大多数都是通过论文当中提供的公式来进行实现的，少部分发现了公式在面对一些不太友好数据的情况会出现输出维度不同的问题，增加了padding的计算方法。

本着不重复造轮子的原则，在我使用的PyTorch-1.5.0当中提供了AdaptiveMaxPool2d和AdaptiveAvgPool2d方法，直接采用其进行构造，代码逻辑会更为清晰和行数也会更短。

同时提供一个outputdim的辅助函数，通过输入的之前卷积层结果的channel数来计算输出维度。

import torch
import torch.nn as nn

class SpatialPyramidPooling(nn.Module):
    def __init__(self, levels = 3, pooling='max'):
        super(SpatialPyramidPooling, self).__init__()
        self.levels = levels
        self.mode = pooling
        self.pooling_method = nn.AdaptiveMaxPool2d if pooling == 'max' else nn.AdaptiveAvgPool2d
        self.layers = [self.pooling_method(i) for i in range(1, levels+1)]
        
    def forward(self, x):
        b, c, _, _ = x.size()
        pooled = []
        for p in self.layers:
            pooled.append(p(x).view(b, -1))
        return torch.cat(pooled, -1)
    
    def outputdim(self, previous_channel):
        return previous_channel * sum([i*i for i in range(1, self.levels+1)])

测试如下：

spp = SpatialPyramidPooling()
input = torch.randn(8, 32, 224, 224)
output = spp(input)
print(output.shape)

input = torch.randn(8, 32, 128, 324)
output = spp(input)
print(output.shape)

输出结果为：

1 2	torch.Size([8, 448]) torch.Size([8, 448])

的确将不同大小的输入给调整成了统一大小。

Codeforces 1368E - Ski Accidents

发表于 2020-07-14

原文

Arthur owns a ski resort on a mountain. There are $n$ landing spots on the mountain numbered from $1$ to $n$ from the top to the foot of the mountain. The spots are connected with one-directional ski tracks. All tracks go towards the foot of the mountain, so there are no directed cycles formed by the tracks. There are at most two tracks leaving each spot, but many tracks may enter the same spot.

A skier can start skiing from one spot and stop in another spot if there is a sequence of tracks that lead from the starting spot and end in the ending spot. Unfortunately, recently there were many accidents, because the structure of the resort allows a skier to go through dangerous paths, by reaching high speed and endangering himself and the other customers. Here, a path is called dangerous, if it consists of at least two tracks.

Arthur wants to secure his customers by closing some of the spots in a way that there are no dangerous paths in the resort. When a spot is closed, all tracks entering and leaving that spot become unusable.

Formally, after closing some of the spots, there should not be a path that consists of two or more tracks.

Arthur doesn’t want to close too many spots. He will be happy to find any way to close at most $\frac47n$ spots so that the remaining part is safe. Help him find any suitable way to do so.

Input

The first line contains a single positive integer $T$ — the number of test cases. $T$ test case description follows.

The first line of each description contains two integers $n$ and $m$ ( $1\le n\le 2\cdot 10^5$ ) — the number of landing spots and tracks respectively.

The following $m$ lines describe the tracks. Each of these lines contains two integers $x$ and $y$ ( $1\le x< y\le n$ ) — indices of the starting and finishing spots for the respective track. It is guaranteed that at most two tracks start at each spot. There may be tracks in which starting and finishing spots both coincide.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2\cdot 10^5$ .

Output

For each test case, print a single integer $k$ ( $0\le k\le \frac47n$ ) — the number of spots to be closed. In the next line, print $k$ distinct integers — indices of all spots to be closed, in any order.

If there are several answers, you may output any of them. Note that you don’t have to minimize $k$ . It can be shown that a suitable answer always exists.

Example

input

output

Note

In the first sample case, closing any two spots is suitable.

In the second sample case, closing only the spot $1$ is also suitable.

大致意思

给出一个有向无环图，所有定点的出度不超过2，入度不做限制，同时限定边的起始点一定比终止点要小（是从山顶到山脚的滑雪道）。

要求去掉其中的一些顶点（不多于 $\frac47n$ ），使得图中没有长度超过2的路径。

思路

贪心想法为从节点1（山顶）向后分层级来遍历，如果是第一条连边则保留，第二条则删除相关联节点。

如之后代码中所表示的level，这里通过level将所有顶点分成三类，下标为节点对应的level，形式化表述如下：

$V_0$ 包含只拥有来自 $V_2$ 入边的顶点
$V_1$ 包含至少有一条来自 $V_0$ 入边，但是没有来自 $V_1$ 入边的顶点
$V_2$ 包含至少有一条来自 $V_1$ 入边的顶点

对应的就是删除所有 $V_2$ 中的顶点，下面来证明为什么可以保证不超过 $\frac47n$ ：

由于 $V_2$ 至少有一条来自 $V_1$ 的边，而一个顶点最多两条出边，所以最多有 $2|V_1|$ 条出边，那么有着 $|V_2|\le 2|V_1|$ ，同理有着 $|V_1|\le 2|V_0|$ 。于是 $n = |V_0|+|V_1|+|V_2|\ge \frac74|V_2|$ ，所以 $|V_2|\le \frac47n$ 。

只需要从山顶到山脚扫描一遍就可以确定哪些是 $|V_2|$ 当中的顶点，这里的时间复杂度为 $O(n)$ 。

注意：如果对整个level数组进行memset操作，有一个 $t=2\cdot 10^5$ 的case会超时！

代码

#include <bits/stdc++.h>
using namespace std;

#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define ll long long
#define maxn 200010

int level[maxn];
vector<int> adj[maxn];

int main(){
    IOS;
    int t;
    cin>>t;
    while(t--){
        int n, m;
        cin>>n>>m;
        for(int i=0;i<m;++i){
            int x, y;
            cin>>x>>y;
            adj[y].push_back(x);
        }
        vector<int> ans;
        for(int u=1;u<=n;++u){
            for(int v: adj[u]){
                level[u] = max(level[u], (level[v]+1)%3);
            }
            if(level[u] == 2){
                ans.push_back(u);
            }
        }

        cout<<ans.size()<<endl;
        for(auto i: ans){
            cout<<i<<' ';
        }
        cout<<endl;
        
        memset(level, 0, sizeof(int)*(n+1));
        for(int i=1;i<=n;++i)
            adj[i].clear();
    }
}

2019大数据研究中心夏令营上机考试题解

发表于 2020-07-07

因为就是准备笔试时候自己刷了刷题，所以基本都只在本地跑过了样例

1.最近点对

Implementation

#include<bits/stdc++.h>
using namespace std;

#define maxn 10010
#define ll long long

ll x[maxn], y[maxn];

ll dist(ll x1, ll y1, ll x2, ll y2){
    return (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
}

int main(){
    int t;
    cin>>t;
    while(t--){
        int n;
        ll mindist = 0x7fffffff;
        cin>>n;
        for(int i=0;i<n;++i){
            cin>>x[i]>>y[i];
            for(int j=0;j<i;++j){
                mindist = min(mindist, dist(x[i], y[i], x[j], y[j]));
            }
        }
        cout<<mindist<<endl;
    }
}

2. 病人排队

Implementation

#include<bits/stdc++.h>
using namespace std;

#define ll long long

struct person{
    string id;
    int age;
    int order;
    person(string id, int age, int order):
    id(id), age(age), order(order){};
};

bool operator< (const person a, const person b){
    if(a.age>=60 && b.age<60){
        return false;
    }
    else if(a.age<60 && b.age>=60){
        return true;
    }
    else if(a.age>=60 && b.age>=60){
        if(a.age != b.age){
            return a.age < b.age;
        }
        else{
            return a.order > b.order;
        }
    }
    else{
        return a.order > b.order;
    }
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    int n;
    cin>>n;
    priority_queue<person> q;
    for(int i=0;i<n;++i){
        string id;
        int age;
        cin>>id>>age;
        q.push(person(id, age, i));
    }
    while(!q.empty()){
        auto tmp = q.top();
        q.pop();
        cout<<tmp.id<<endl;
    }
}

3. 网线主管

Binary Search

#include<bits/stdc++.h>
using namespace std;

#define maxn 10010
#define ll long long

int len[maxn];
int n, k;

bool test(int l){
    int cnt = 0;
    for(int i=0;i<n;++i){
        cnt += len[i] / l;
    }
    return cnt >= k;
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin>>n>>k;
    for(int i=0;i<n;++i){
        double tmp;
        cin>>tmp;
        len[i] = round(tmp * 100);
    }

    if(!test(1)){
        cout<<"0.00"<<endl;
        return 0;
    }

    int l = 1, r = 10000001;
    while(r - l > 1){
        int mid = (l + r) >> 1;
        if(test(mid)){
            l = mid;
        }
        else{
            r = mid;
        }
    }
    printf("%.2lf\n", ((double)l/100));
}

4. 棋盘问题

Search

#include<bits/stdc++.h>
using namespace std;

int n, k;
int res;
char mat[10][10];
int col[10];

bool isok(int r, int c){
    for(int i=0;i<r;++i){
        if(col[i] == c){
            return false;
        }
    }
    return true;
}

void solve(int r, int rest){
    if(rest == 0){
        ++res;
        return;
    }
    if(r == n){
        return;
    }
    for(int i=0;i<n;++i){
        if(mat[r][i] == '#' && isok(r, i)){
            col[r] = i;
            solve(r+1, rest-1);
        }
    }
    col[r] = -1;
    solve(r+1, rest);
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    while(cin>>n>>k && n!=-1 && k !=-1){
        for(int i=0;i<n;++i){
            cin>>mat[i];
        }
        res = 0;
        solve(0, k);
        cout<<res<<endl;
    }
}

5. 移动办公

DP

#include<bits/stdc++.h>
using namespace std;

#define maxn 101

int p[maxn], n[maxn];
int dp[2][maxn];

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    int t, m;
    cin>>t>>m;
    for(int i=0;i<t;++i){
        cin>>p[i]>>n[i];
    }

    dp[0][t] = dp[1][t] = 0;
    for(int i=t-1;i>=0;--i){
        dp[0][i] = max(dp[0][i+1]+p[i], dp[1][i+1]+p[i]-m);
        dp[1][i] = max(dp[1][i+1]+n[i], dp[0][i+1]+n[i]-m);
    }

    cout<<max(dp[0][0], dp[1][0])<<endl;
}

6. 螺旋加密

Implementation

#include<bits/stdc++.h>
using namespace std;

int row, col;
char mat[24][24];

string getcode(char c){
    if(c == ' '){
        return "00000";
    }
    int n = c - 'A' + 1;
    string res;
    for(int i=0;i<5;++i){
        if(n & 1){
            res.push_back('1');
        }
        else{
            res.push_back('0');
        }
        n >>= 1;
    }
    reverse(res.begin(), res.end());
    return res;
}

void fillblock(const string & code){
    for(int i=0;i<24;++i){
        for(int j=0;j<24;++j){
            mat[i][j] = '0';
        }
    }

    int u = 0, d = row-1, l = 0, r = col-1;
    int i = 0, j = 0;
    int dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    int dd = 0;
    for(int k=0;k<code.length();++k){
        mat[i][j] = code[k];
        if(j + dir[dd][1] > r){
            ++u;
            dd=1;
        }
        else if(j + dir[dd][1] < l){
            --d;
            dd=3;
        }
        else if(i + dir[dd][0] > d){
            --r;
            dd=2;
        }
        else if(i + dir[dd][0] < u){
            ++l;
            dd=0;
        }
        i += dir[dd][0];
        j += dir[dd][1];
    }
}


int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin>>row>>col;
    string s;
    getline(cin, s);

    string mycode = "";
    for(int i=1;i<s.length();++i){
        mycode += getcode(s[i]);
    }

    fillblock(mycode);
    for(int i=0;i<row;++i){
        for(int j=0;j<col;++j){
            cout<<mat[i][j];
        }
    }
    cout<<endl;
}

7. 单词序列

BFS

#include<bits/stdc++.h>
using namespace std;

int row, col;
char mat[24][24];
map<string, int> dist;

bool diff1(const string& a, const string& b){
    int len = a.length();
    int cnt = 0;
    for(int i=0;i<len;++i){
        if(a[i] != b[i]){
            ++cnt;
        }
    }
    return cnt == 1;
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    string s, e;
    cin>>s>>e;
    dist[s] = 1;
    dist[e] = 42;
    string t;
    while(cin>>t){
        dist[t] = 42;
    }

    queue<string> q;
    q.push(s);
    while(!q.empty()){
        string v = q.front();
        q.pop();
        for(auto tmp: dist){
            if(tmp.second == 42 && diff1(tmp.first, v)){
                dist[tmp.first] = dist[v] + 1;
                q.push(tmp.first);
            }
        }
    }
    if(dist[e] == 42){
        cout<<0<<endl;
    }
    else{
        cout<<dist[e]<<endl;
    }
}

8. 区间异或和

Binary Indexed Tree

#include<bits/stdc++.h>
using namespace std;

#define maxn 100010

int n, q;
int arr[maxn], nums[maxn];

int lb(int x){
    return x & (-x);
}

void update(int k, int x){
    for(int i=k;i<=n;i+=lb(i))
        arr[i] ^= x;
}

int getsum(int k){
    int res = 0;
    for(int i=k;i>0;i-=lb(i))
        res ^= arr[i];
    return res;
}

int main(){
    while(cin>>n>>q){
        memset(arr, 0, sizeof(arr));
        int res = 0;
        for(int i=1;i<=n;++i){
            update(i, i);
            nums[i] = i;
        }
        for(int i=0;i<q;++i){
            int op, l, r;
            cin>>op>>l>>r;
            if(op){
                update(l, r ^ nums[l]);
                nums[i] = r;
            }
            else{
                res ^= getsum(r) ^ getsum(l-1);
            }
        }
        cout<<res<<endl;
    }
}

9. 炮兵阵地

DP

#include<bits/stdc++.h>
using namespace std;
int n, m;
char grid[104][10];
int row[104];
int state[104];
int countone[104];
int dp[104][64][64];

int count_one(int k)
{
	int cnt = 0;
	while (k)
	{
		++cnt;
		k = k & (k - 1);
	}
	return cnt;
}

int preprocess()
{
	int cnt = 0;
	for (int i = 0; i < (1 << m); ++i)
	{
		if ((i&(i >> 1)) == 0 && (i&(i >> 2)) == 0)
		{
			countone[cnt] = count_one(i);
			state[cnt++] = i;
		}
	}
	return cnt;
}

int main()
{
	cin >> n >> m;
	int ms = preprocess();
	for (int i = 0; i < n; ++i)
		cin >> grid[i];
	for (int i = 0; i < n; ++i)
		for (int j = 1; j <= m; ++j)
			row[i+1] += (grid[i][j-1] == 'P') << (m - j);
	for (int j = 0; j < ms; ++j)
		if ((state[j] | row[1]) == row[1])
			dp[1][0][j] = countone[j];
	for (int i = 2; i <= n; ++i)
	{
		for (int ppre = 0; ppre < ms; ++ppre)
		{
			if ((state[ppre] | row[i - 2]) != row[i - 2])
				continue;
			for (int pre = 0; pre < ms; ++pre)
			{
				if ((state[pre] | row[i - 1]) != row[i - 1] || (state[ppre] & state[pre]) != 0)
					continue;
				for (int j = 0; j < ms; ++j)
					if ((state[j] | row[i]) == row[i] && (state[j] & state[pre]) == 0 && (state[j] & state[ppre]) == 0)
						dp[i][pre][j] =max(dp[i][pre][j], countone[j]+ dp[i - 1][ppre][pre]);
			}
		}
	}
	int ans = 0;
	for (int i = 0; i < ms; ++i)
		for (int j = 0; j < ms; ++j)
			ans = max(ans,dp[n][i][j]);
	cout << ans << endl;
}

a. 迷宫路口

DFS

#include<bits/stdc++.h>
using namespace std;

int s, n;
int cnt[12];
int mat[32][32];

bool can_place(int x, int y, int size){
    if(x+size<=s && y+size<=s){
        for(int i=0;i<size;++i){
            for(int j=0;j<size;++j){
                if(mat[x+i][y+j] != 0){
                    return false;
                }
            }
        }
        return true;
    }
    else{
        return false;
    }
}

void place(int x, int y, int size){
    for(int i=0;i<size;++i){
        for(int j=0;j<size;++j){
            mat[x+i][y+i] = size;
        }
    }
    --cnt[size];
}

void unplace(int x, int y){
    int size = mat[x][y];
    for(int i=0;i<size;++i){
        for(int j=0;j<size;++j){
            mat[x+i][y+j] = 0;
        }
    }
    ++cnt[size];
}

pair<int, int> next_loc(int x, int y){
    for(int i=x;i<s;++i){
        for(int j=y;j<s;++j){
            if(mat[i][j] == 0){
                return make_pair(i, j);
            }
        }
    }
    return make_pair(-1, -1);
}

bool dfs(int x, int y){
    for(int i=10;i>=1;--i){
        if(cnt[i]){
            if(can_place(x, y, i)){
                place(x, y, i);
                auto loc = next_loc(x, y);
                if(loc.first == -1 && loc.second == -1){
                    return true;
                }
                if(dfs(loc.first, loc.second)){
                    return true;
                }
                unplace(x, y);
            }
        }
    }
    return false;
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    int t;
    cin>>t;
    while(t--){
        cin>>s>>n;
        for(int i=0;i<n;++i){
            int tmp;
            cin>>tmp;
            cnt[tmp]++;
        }
        cout<<(dfs(0, 0)? "YES": "NO")<<endl;
    }
}

2018大数据研究中心夏令营上机考试题解

发表于 2020-07-07

因为就是准备笔试时候自己刷了刷题，所以基本都只在本地跑过了样例

A. 第n小的质数

Implementation

#include<bits/stdc++.h>
using namespace std;

#define maxn 200010

bool isprime[maxn];
vector<int> primes;

void solve(){
    fill(isprime, isprime+maxn, true);
    int k=2;
    while(k<maxn-1){
        for(int i=2*k;i<maxn-1;i+=k){
            isprime[i] = false;
        }
        for(++k;!isprime[k];++k){
            ;
        }
    }
    for(int i=2;i<maxn;++i){
        if(isprime[i]){
            primes.push_back(i);
        }
    }
}


int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    solve();

    int n;
    cin>>n;
    cout<<primes[n-1]<<endl;
}

B. 潜伏者

Implementation

#include<bits/stdc++.h>
using namespace std;

map<char, char> trans;

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    string s, t;
    cin>>s>>t;
    bool failed = false;
    for(int i=0;i<s.length();++i){
        if(trans.find(s[i]) != trans.end() && trans[s[i]] != t[i]){
            failed = true;
            break;
        }
        else{
            trans[s[i]] = t[i];
        }
    }

    for(int i=0;i<26;++i){
        if(trans.find('A'+i) == trans.end()){
            failed = true;
            break;
        }
    }
    
    cin>>s;
    if(failed){
        cout<<"Failed"<<endl;
    }
    else{
        for(int i=0;i<s.length();++i){
            cout<<trans[s[i]];
        }
        cout<<endl;
    }

}

C. 逃离迷宫

BFS

#include<bits/stdc++.h>
using namespace std;

int m, t;
char mat[12][12];
int cnt[12][12];
int sx, sy, ex, ey;
int dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    int k;
    cin>>k;
    while(k--){
        cin>>m>>t;
        for(int i=0;i<m;++i){
            for(int j=0;j<m;++j){
                cin>>mat[i][j];
                if(mat[i][j] == 'S'){
                    sx = i;
                    sy = j;
                }
                if(mat[i][j] == 'E'){
                    ex = i;
                    ey = j;
                }
            }
        }

        queue<pair<int, int>> q;
        for(int i=0;i<m;++i){
            for(int j=0;j<m;++j){
                cnt[i][j] = -1;
            }
        }
        q.push(make_pair(sx, sy));
        cnt[sx][sy] = 0;
        while(!q.empty()){
            int x = q.front().first;
            int y = q.front().second;
            q.pop();

            for(int i=0;i<4;++i){
                int nx = x + dir[i][0];
                int ny = y + dir[i][1];
                if(0 <= nx && nx < m && 0 <= ny && ny < m && (mat[nx][ny] == '.' || mat[nx][ny] == 'E') && cnt[nx][ny] == -1){
                    cnt[nx][ny] = cnt[x][y] + 1;
                    q.push(make_pair(nx, ny));
                }
            }
        }

        if(cnt[ex][ey] == -1 || cnt[ex][ey] > t){
            cout<<"NO"<<endl;
        }
        else{
            cout<<"YES"<<endl;
        }
    }
}

D. 跑步

DP

#include<bits/stdc++.h>
using namespace std;

#define maxn 10010
#define maxm 502

int n, m;
int d[maxn];
int dp[maxn][maxm];

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin>>n>>m;
    for(int i=0;i<n;++i){
        cin>>d[i];
    }

    for(int i=0;i<n;++i){
        for(int j=0;j<m;++j){
            dp[i][j] = -1;
        }
    }

    dp[0][0] = 0;

    for(int i=0;i<n;++i){
        for(int j=0;j<=m;++j){
            if(dp[i][j] != -1){
                if(j<m){
                    dp[i+1][j+1] = max(dp[i+1][j+1], dp[i][j] + d[i]);
                }
                if(i+j <= n){
                    dp[i+j][0] = max(dp[i+j][0], dp[i][j]);
                }
                if(j == 0){
                    dp[i+1][0] = max(dp[i+1][0], dp[i][0]);
                }
            }
        }
    }
    
    cout<<dp[n][0]<<endl;
}

E. What time is it?

Implementation

#include<bits/stdc++.h>
using namespace std;

string s[3];

bool check_num(int num, int idx){
    switch (num)
    {
    case 0:
        return s[1][idx+1]==' ';
    case 1:
        return s[0][idx+1]==' '&&s[1][idx]==' '&&s[1][idx+1]==' '&&s[2][idx]==' '&&s[2][idx+1]==' ';
    case 2:
        return s[1][idx]==' '&&s[2][idx+2]==' ';
    case 3:
        return s[1][idx]==' '&&s[2][idx]==' ';
    case 4:
        return s[0][idx+1]==' '&&s[2][idx]==' '&&s[2][idx+1]==' ';
    case 5:
        return s[1][idx+2]==' '&&s[2][idx]==' ';
    case 6:
        return s[1][idx+2]==' ';
    case 7:
        return s[1][idx]==' '&&s[1][idx+1]==' '&&s[2][idx]==' '&&s[2][idx+1]==' ';
    case 8:
        return true;
    case 9:
        return s[2][idx]==' ';
    default:
        return false;
    }
}

bool check_time(int hour, int minute, int idx){
    return check_num(hour/10, idx) && check_num(hour%10, idx+3) && check_num(minute/10, idx+6) && check_num(minute%10, idx+9);
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    int t;
    cin>>t;
    getline(cin, s[0]);
    while(t--){
        for(int i=0;i<3;++i){
            getline(cin, s[i]);
        }
        int ans = -1;

        for(int hour=0;hour<24;++hour){
            for(int minute=0;minute<59;++minute){
                int delayminute = minute + 15;
                int delayhour = hour + (delayminute / 60);
                delayminute %= 60;
                delayhour %= 24;
                if(check_time(hour, minute, 0) && check_time(delayhour, delayminute, 13)){
                    if(ans == -1){
                        ans = hour * 100 + minute;
                    }
                    else{
                        ans = -2;
                    }
                }
            }
        }
        if(ans >= 0){
            printf("%04d\n", ans);
        }
        else{
            printf("Not Sure\n");
        }
    }
}

F. Sorting It All Out

Sortings

#include<bits/stdc++.h>
using namespace std;

int edge[26][26];
int indeg[26], outdeg[26];
int n, m;
bool is_unique, no_circle;

string test(){
    memset(indeg, 0, sizeof(indeg));
    memset(outdeg, 0, sizeof(outdeg));
    is_unique = true;
    no_circle = true;
    string res;

    for(int i=0;i<n;++i){
        for(int j=0;j<n;++j){
            if(edge[i][j]){
                ++outdeg[i];
                ++indeg[j];
            }
        }
    }

    while(true){
        int tmp = -1;
        for(int i=0;i<n;++i){
            if(indeg[i] == 0){
                if(tmp == -1){
                    tmp = i;
                }
                else{
                    is_unique=false;
                }
            }
        }
        if(tmp == -1){
            break;
        }
        res.push_back('A'+tmp);
        indeg[tmp] = -1;
        for(int i=0;i<n;++i){
            if(edge[tmp][i]){
                --indeg[i];
            }
        }
    }

    for(int i=0;i<n;++i){
        if(indeg[i] != -1){
            no_circle = false;
        }
    }
    return res;
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    while(cin>>n>>m, n && m){
        bool finished = false;
        memset(edge, 0, sizeof(edge));
        for(int i=0;i<m;++i){
            char a, c, b;
            cin>>a>>c>>b;
            if(finished){
                continue;
            }
            edge[a-'A'][b-'A'] = 1;
            string res = test();
            if(!no_circle){
                finished = true;
                cout<<"Inconsistency found after "<<i+1<<" relations."<<endl;
            }
            if(no_circle && is_unique){
                finished = true;
                cout<<"Sorted sequence determined after "<<i+1<<" relations: "<<res<<"."<<endl;
            }
        }
        if(!finished){
            cout<<"Sorted sequence cannot be determined."<<endl;
        }
    }
}

G. Rails

Stack

#include<bits/stdc++.h>
using namespace std;

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    stack<int> s;
    int n;
    while(cin>>n, n){
        while(true){
            bool impossible = false;
            int cnt = 1;
            while(!s.empty()){
                s.pop();
            }
            for(int i=0;i<n;++i){
                int tmp;
                cin>>tmp;
                if(i==0 && tmp == 0){
                    goto end_loop;
                }
                if(impossible){
                    continue;
                }
                while(s.empty() || s.top() < tmp){
                    s.push(cnt);
                    ++cnt;
                }
                if(s.top() == tmp){
                    s.pop();
                }
                else{
                    impossible = true;
                }
            }
            cout<<(impossible? "No":"Yes")<<endl;
        }
        end_loop:
            cout<<endl;
    }
}

H. The Rotation Game

IDA*

#include<bits/stdc++.h>
using namespace std;

int opposite[8] = { 5, 4, 7, 6, 1, 0, 3, 2 };
int maxdepth;
int line[8][7] = {
	{ 0, 2, 6, 11, 15, 20, 22 },
    { 1, 3, 8, 12, 17, 21, 23 },
    { 10, 9, 8, 7, 6, 5, 4 },
    { 19, 18, 17, 16, 15, 14, 13 },
    { 23, 21, 17, 12, 8, 3, 1 },
    { 22, 20, 15, 11, 6, 2, 0 },
    { 13, 14, 15, 16, 17, 18, 19 },
    { 4, 5, 6, 7, 8, 9, 10 }
};
string ans;
int circle[8] = { 6,7,8,11,12,15,16,17 };
int board[24];

int estimate()
{
	int cnt[4] = { 0 }, ans = 0;
	for (int i = 0; i<8; ++i)
		ans = max(ans, ++cnt[board[circle[i]]]);
	return 8 - ans;
}

void doit(int op)
{
  int temp = board[line[op][0]];
  for (int i = 0; i<6; ++i)
    board[line[op][i]] = board[line[op][i + 1]];
  board[line[op][6]] = temp;
}

bool dfs(int depth)
{
	int guess = estimate();
	if (guess == 0)
		return true;
	else if (depth + guess>maxdepth)
		return false;
	for (int i = 0; i<8; ++i)
	{
		doit(i);
		ans.push_back('A' + i);
		if (dfs(depth + 1))
			return true;
		ans.pop_back();
		doit(opposite[i]);
	}
	return false;
}

void ida()
{
	for (int i = 1;; ++i)
	{
		maxdepth = i;
		if (dfs(0))
			break;
	}
}

int main()
{
	while (cin >> board[0], board[0])
	{
		ans.clear();
		for (int i = 1; i<24; ++i)
			cin >> board[i];
		if (estimate() == 0)
		{
			cout << "No moves needed" << endl;
			cout << board[7] << endl;
		}
		else
		{
			ida();
			cout << ans << endl;
			cout << board[7] << endl;
		}
	}
}

Python使用logger保存训练参数日志

发表于 2020-07-06

在神经网络训练过程当中，如果是利用jupyter-notebook来进行代码编写的话，可能断开之后不会看到输出的结果。利用logging模块可以将内容同时输出到文件和终端，首先定义构造logger的函数内容如下：

import logging

def get_logger(filename, verbosity=1, name=None):
    level_dict = {0: logging.DEBUG, 1: logging.INFO, 2: logging.WARNING}
    formatter = logging.Formatter(
        "[%(asctime)s][%(filename)s][line:%(lineno)d][%(levelname)s] %(message)s"
    )
    logger = logging.getLogger(name)
    logger.setLevel(level_dict[verbosity])

    # Output to file
    fh = logging.FileHandler(filename, "w")
    fh.setFormatter(formatter)
    logger.addHandler(fh)

    # Output to terminal
    sh = logging.StreamHandler()
    sh.setFormatter(formatter)
    logger.addHandler(sh)

    return logger

之后在训练流程当中通过以上的函数生成logger，再采用info方法进行保存就可以了：

logger = get_logger('./train.log')

logger.info('start training!')
for epoch in range(EPOCHS):
    ...
    loss = ...
    acc = ...
    logger.info('Epoch:[{}/{}]\t loss={:.5f}\t acc={:.3f}'.format(epoch, EPOCHS, loss, acc))
    ...
logger.info('finish training!')

[论文笔记] Deep Gradient Compression: Reducing the Communication Bandwidth for Distributed Training

发表于 2020-07-05

Introduction

正常的分布式训练方法会传递所有的梯度，但是实际上，可能有超过99%的梯度交换都是无关紧要的，所以可以通过只传送重要的梯度来减少在深度学习的分布式训练当中通信带宽。DGC方法通过稀疏更新来只传递重要的梯度，同时利用Momentum Correction，Gradient Clipping等方法来预防不收敛的情形，保证分布式训练不会影响最终的模型准确性。

Deep Gradient Compression

Gradient Sparsification

那么如何来衡量一个梯度的重要性呢，显然如果一个网络节点的梯度大小绝对值更大的话，它会带来的权重更新就会更大，那么对于整个网络的变化趋势而言，就是更为重要的。在DGC方法当中，认为绝对值大小超过某一阈值的梯度为重要的梯度。但是如果只传递此类重要梯度的话，和损失函数的优化目标会存在一定程度上的差距，所以出于减少信息损失的考虑，把剩下不重要的梯度在本地进行累积，那么只要时间足够，最终累积梯度就会超过所设定的阈值，进行梯度交换。

由于仅仅是数值较大的梯度进行了立即传递，较小的梯度在本地进行累积更新，所以能够极大减少每个step交换梯度所需要的通信带宽。那么需要考虑的一点是这种本地梯度累积的方法是否会对于优化目标产生影响，计 $f(\cdot)$ 为损失函数，可以首先分析一个step的更新公式如下：

$w_{t+1}^{(i)} = w_{t}^{(i)}- \eta \frac{1}{Nb}\sum_{k=1}^N \sum_{x\in \mathcal{B}_{k,t}}\nabla^{(i)}f(x,w_t)$

如果在本地进行梯度累积，那么假设在经历过 $T$ 个step之后才进行梯度交换，那么更新公式可以修改为如下形式：

$\begin{aligned} w_{t+T}^{(i)} &= w_{t}^{(i)}- \eta \frac{1}{Nb}\sum_{k=1}^N \sum_{\tau= 0}^{T-1}\sum_{x\in \mathcal{B}_{k,t}}\nabla^{(i)}f(x,w_{t+\tau}) \\ &= w_{t}^{(i)} - \eta T \frac{1}{NbT}\sum_{k=1}^N \left(\sum_{\tau= 0}^{T-1}\sum_{x\in \mathcal{B}_{k,t}}\nabla^{(i)}f(x,w_{t+\tau})\right) \end{aligned}$

那么如上式所示，可以发现当针对于 $T$ 大小进行学习率缩放之后，在分子分母的 $T$ 可以消去，于是总体可以看成是人为的将batch大小从 $Nb$ 提升到了 $NbT$ 。所以直观上本地梯度累积的方法可以看成是随着更新时间区间的拉长来增大训练batch的大小，同时对于学习率进行同比例缩放，并不会影响最终的优化目标。

Momentum Correction

如果直接针对于普通的SGD采用以上的DGC方法，那么先让当更新十分稀疏，即间隔区间长度 $T$ 很大的时候，可能会影响网络的收敛。所以又提出了Momentum Correction和Local Gradient的方法来缓解对于收敛性质的伤害。

最普通的动量方法如下所示，其中 $m$ 的值即为动量。

$u_{t+1} = mu_t + \sum_{k=1}^N \nabla_{k,t},\quad w_{t+1} = w_t - \eta u_t$

事实上最终进行本地的梯度累积和更新都是利用左侧的 $u_t$ 来代替原始梯度 $\nabla_t$ 的，于是可以得到参数更新的表达式如下，假设稀疏更新的时间间隔为 $T$ 。

$\begin{aligned} w_{t+T} ^{(i)} &= w_t^{(i)} - \eta\sum_{k=1}^N\left( \sum_{\tau=0}^{T-1}u_t \right) \\ &= w_t^{(i)} - \eta\sum_{k=1}^N\left[ \left(\sum_{\tau=0}^{T-1}m^\tau\right)\nabla_{k,t}^{(i)}+ \left(\sum_{\tau=0}^{T-2}m^\tau\right)\nabla_{k,t+1}^{(i)} +\ldots\right] \end{aligned}$

对比没有动量修正的更新方法如下：

$\begin{aligned} w_{t+T} ^{(i)} &= w_t^{(i)} - \eta\sum_{k=1}^N\left[\nabla_{k,t}^{(i)}+ \nabla_{k,t+1}^{(i)} +\ldots\right] \end{aligned}$

可以发现实际上缺少了 $\sum_{\tau=0}^{T-1}m^\tau$ 的求和项，当 $m$ 为0的时候得到的就是普通情形。直观上来理解可以认为越早的梯度提供了一个更大的权重。这是合理的是因为在进行梯度交换更新之后，本地参数和全局参数是相同的，而随着本地更新时间的增加，本地参数同全局参数的差异会越来越大，那么对于所得到梯度全局的影响的泛化性应当越来越差，所以理应当赋予一个更小的权重。

Local Gradient Clipping

梯度裁剪即在梯度的L2范数超过一个阈值的时候,对梯度进行一个缩放,来防止梯度爆炸的问题。通常而言,分布式训练的梯度裁剪是在进行梯度累积之后进行,然后利用裁剪过后的梯度进行更新,并分发新的网络权重给其他的训练节点。但是在DGC方法中将梯度的传送稀疏化了,同时存在本地更新,这种先汇总后裁剪的方法就不可取。这里的梯度裁剪是再将新的梯度累加到本地之前就进行。

需要做一个假设如下,假设 $N$ 个训练节点的随机梯度为独立同分布，都有着方差 $\sigma^2$ ，那么可以知道所有训练节点的梯度汇总之后，总的梯度应当有方差 $N\sigma^2$ ，于是单个运算节点的梯度和总梯度有关系如下：

$E[||G^k||_2]\approx\sigma , \quad E[||G||_2] \approx N^{1/2}\sigma \Rightarrow E[||G^k||_2]\approx N^{-1/2}E[||G||_2]$

所以应当对于所设定的阈值进行一个缩放，假设原本设定的梯度的L2范数的阈值为 $thr_{G}$ 的话，那么对于每一个训练节点而言，其阈值应当为：

$thr_{G^k} = N^{-1/2}thr_G$

其中的 $N$ 表示的是训练节点的个数。

Overcoming the Staleness Effect

事实上由于梯度在本地进行累积，可能更新的时候梯度是过时的了(stale)，在实验中发现绝大部分的梯度都在600～1000次迭代之后才会更新。文章中提出了两种方法来进行改善。

Momentum Factor Masking

将 $v$ 记作在本地的梯度累积：

$v_{k,t} = v_{k,t-1} + u_{k,t}$

可以利用Momentum Factor Masking的方法，这里简单起见，对于梯度 $u$ 和累积梯度 $v$ 采用同样的Mask：

$\begin{aligned} Mask \leftarrow|v_{k,t}| > thr \\ v_{k,t}\leftarrow v_{k,t}\odot \neg Mask \\ u_{k,t}\leftarrow u_{k,t}\odot \neg Mask \end{aligned}$

这个方法会让过于老的梯度来停止累积，防止过于旧的梯度影响模型的优化方向。

Warm-up Training

在训练的最初期，模型往往变化的特别剧烈，这时候采用DGC的问题如下：

稀疏更新会限制模型变化的范围，使得这个剧烈变化的时段变得更长。
早期留在本地的梯度，可能和实际的优化方向并不符合，在后面传递可能会把模型引入错误的方向。

所以采用Warm-up的训练trick，在一开始采用更低的学习率，同时采用更低的稀疏更新的阈值，减少被延缓传递的参数。这里在训练的最开始采用一个很低的学习率，然后以指数形式逐渐增加到默认值。