在Spirit Qi中使用std::shared_ptr对象

发表于 2024-12-09

boost::spirit::qi是一个用于解析字符串的库，可以用于解析字符串并构造对象。在解析的过程中，有时候需要构造语法树，这个时候通常可以采用phx::new_或者phx::construct来构造裸指针或对象。但是在实际的应用当中，有时候会希望通过如std::shared_ptr这样的智能指针来管理对象的生命周期，但是在boost::phoenix当中并没有提供make_shared这样的函数对象。

基于stackoverflow上的回答可以构造一个make_shared_的函数对象，用于在boost::spirit::qi的语法规则当中延迟构造std::shared_ptr对象。

namespace boost::phoenix {
template <typename T>
struct make_shared_f {
  template <typename... A>
  struct result {
    typedef std::shared_ptr<T> type;
  };

  template <typename... A>
  typename result<A...>::type operator()(A&&... a) const {
    return std::make_shared<T>(std::forward<A>(a)...);
  }
};
template <typename T>
using make_shared_ = function<make_shared_f<T>>;
}  // namespace boost::phoenix

在使用的时候可以如下构造创建std::shared_ptr对象的action：

namespace qi = boost::spirit::qi;
namespace phx = boost::phoenix;

using phx::make_shared_;
using qi::_1;
using qi::_val;

...

expr = term[_val = _1] >>
       *(('+' >> term[_val = make_shared_<AddNode>()(_val, _1)]) |
         ('-' >> term[_val = make_shared_<SubNode>()(_val, _1)]));

在Ubuntu系统中安装最新的CMake&GCC工具

发表于 2024-12-09

期望能够在WSL当中使用C++23的特性，所以需要安装最新的CMake和GCC工具，在Ubuntu22.04版本中，默认支持的CMake版本为3.22，GCC版本为11，所以需要安装最新的版本，这里记录一下安装的过程。

CMake

sudo apt-get update
sudo apt-get install apt-transport-https ca-certificates gnupg software-properties-common wget

wget -O - https://apt.kitware.com/keys/kitware-archive-latest.asc 2>/dev/null | sudo apt-key add -
sudo apt-add-repository "deb https://apt.kitware.com/ubuntu/ $(lsb_release -cs) main"
sudo apt-get update

sudo apt-get install cmake

GCC

sudo add-apt-repository ppa:ubuntu-toolchain-r/test
sudo apt-get update
sudo apt-get install gcc-?? g++-??

gcc-?? --version

其中的??代表版本号，例如gcc-13，g++-13

VSCode Ruff插件配置

发表于 2024-06-11

Ruff是一个基于Rust开发的代码格式化工具，其功能类似于black，但是效率上由于基于Rust的原因，要比black快很多，同时也可以支持类似isort的功能。

在VSCode中使用Ruff的时候，可以通过应用商店搜索Ruff插件进行安装，安装完成之后，可以通过以下配置来设置默认的格式化工具：

"[python]": {
    "editor.codeActionsOnSave": {
        "source.organizeImports": "explicit"
    },
    "editor.formatOnType": true,
    "editor.defaultFormatter": "charliermarsh.ruff",
    "editor.codeActionsOnSave": {
        "source.fixAll": "explicit",
        "source.organizeImports": "explicit"
    }
},
"ruff.format.args": [
    "--line-length=120"
]

以上配置会在保存文件的时候自动进行代码格式化，并且对于所有引入的包进行自动排序，同时通过添加命令行参数，将ruff的格式化行宽设置为120。

NAT模式下的WSL2代理设置

发表于 2024-06-11

配置Windows 11的WSL的时候，发现WSL2的网络配置有一些问题，这里记录一下解决方法。

在安装完Ubuntu系统之后，有一些需要通过代理访问的需求，但是会提示：

1	wsl: 检测到 localhost 代理设置，但未镜像到 WSL。NAT模式下的WSL不支持 localhost 代理设置。

尝试使用网络上提供的解决方案，通过使用/etc/resolv.conf文件获取到Windows的DNS服务器地址，然后进行代理的设置，但是发现并没有什么用。

最终查找发现可以通过ip route show命令来获取到Windows的DNS服务器地址，进而动态设置代理。

set_proxy() {
  host_ip=$(ip route show | grep -i default | awk '{print $3}')
  export http_proxy="http://${host_ip}:7890"
  export https_proxy="http://${host_ip}:7890"
}

unset_proxy() {
  unset http_proxy
  unset https_proxy
}

通过将以上内容加入到.zshrc文件中，就可以通过set_proxy和unset_proxy来动态设置和取消代理了。

Hexo博客备份与迁移

发表于 2023-02-20

这两天计划将之前部署在MacBook上面的博客迁移到实验室的Linux电脑上，并且在上面维护，同时由于hexo推送到github上面的文件并不是原始文件，所以希望做一个文件备份，防止丢失。在这里记录一下相关的操作，避免之后再次迁移的时候需要做重复性的工作。

Hexo博客备份

原本博客对应的repo应当是username.github.io，其中master分支用来管理对应的博客，新建一个backup分支用来存放博客的原始文件。

1
2
3

git add -A
git commit -m "source file backup"
git push -u origin main:backup --force

新机器环境配置

首先安装nvm，然后利用nvm安装node

1	nvm install --lts

之后可以检测是否已经安装成功

1 2	node -v npm -v

确认node环境没有问题之后，我们可以进行hexo的安装

1 2	npm install -g hexo-cli npm install -g hexo

环境安装完成之后就可以尝试在本地重新部署博客，拉取github上面的备份

1	git clone https://github.com/path/to/your/repo

转换到对应的分支

1	git checkout origin/backup

进行对应的环境配置

1	npm install

在本地测试是否博客可以正常部署

1	hexo g && hexo s

更新相关Package

我的博客在部署之后就没有进行过相关包的更新，所以很多包都和最新版本相差较多，可以输入以下命令来查看过时的包。

1	npm outdated

可以看到有许多的包和最新版本已经差别较大，我们这里会尝试进行更新，但是直接更新可能会有依赖相关的问题

Package                         Current  Wanted  Latest  Location                                     Depended by
hexo                              4.2.1   4.2.1   6.3.0  node_modules/hexo                            hexo
hexo-deployer-git                 2.1.0   2.1.0   4.0.0  node_modules/hexo-deployer-git               hexo
hexo-deployer-rsync               1.0.0   1.0.0   2.0.0  node_modules/hexo-deployer-rsync             hexo
hexo-generator-archive            1.0.0   1.0.0   2.0.0  node_modules/hexo-generator-archive          hexo
hexo-generator-category           1.0.0   1.0.0   2.0.0  node_modules/hexo-generator-category         hexo
hexo-generator-feed               2.2.0   2.2.0   3.0.0  node_modules/hexo-generator-feed             hexo
hexo-generator-index              1.0.0   1.0.0   3.0.0  node_modules/hexo-generator-index            hexo
hexo-generator-sitemap            2.1.0   2.2.0   3.0.1  node_modules/hexo-generator-sitemap          hexo
hexo-generator-tag                1.0.0   1.0.0   2.0.0  node_modules/hexo-generator-tag              hexo
hexo-renderer-ejs                 1.0.0   1.0.0   2.0.0  node_modules/hexo-renderer-ejs               hexo
hexo-renderer-markdown-it-plus    1.0.4   1.0.6   1.0.6  node_modules/hexo-renderer-markdown-it-plus  hexo
hexo-server                       1.0.0   1.0.0   3.0.0  node_modules/hexo-server                     hexo

这里首先安装 npm-check-updates，然后用这个工具来确认相关的依赖是否有问题

1 2	npm install -g npm-check-updates ncu

Checking /home/yunchong/Documents/hexo/package.json
[====================] 17/17 100%

 hexo                            ^4.0.0  →  ^6.3.0
 hexo-deployer-git               ^2.1.0  →  ^4.0.0
 hexo-deployer-rsync             ^1.0.0  →  ^2.0.0
 hexo-generator-archive          ^1.0.0  →  ^2.0.0
 hexo-generator-category         ^1.0.0  →  ^2.0.0
 hexo-generator-feed             ^2.2.0  →  ^3.0.0
 hexo-generator-index            ^1.0.0  →  ^3.0.0
 hexo-generator-sitemap          ^2.0.0  →  ^3.0.1
 hexo-generator-tag              ^1.0.0  →  ^2.0.0
 hexo-renderer-ejs               ^1.0.0  →  ^2.0.0
 hexo-renderer-markdown-it-plus  ^1.0.4  →  ^1.0.6
 hexo-server                     ^1.0.0  →  ^3.0.0

利用ncu来更新对应的package.json文件

ncu -u

Upgrading /home/yunchong/Documents/hexo/package.json
[====================] 17/17 100%

 hexo                            ^4.0.0  →  ^6.3.0
 hexo-deployer-git               ^2.1.0  →  ^4.0.0
 hexo-deployer-rsync             ^1.0.0  →  ^2.0.0
 hexo-generator-archive          ^1.0.0  →  ^2.0.0
 hexo-generator-category         ^1.0.0  →  ^2.0.0
 hexo-generator-feed             ^2.2.0  →  ^3.0.0
 hexo-generator-index            ^1.0.0  →  ^3.0.0
 hexo-generator-sitemap          ^2.0.0  →  ^3.0.1
 hexo-generator-tag              ^1.0.0  →  ^2.0.0
 hexo-renderer-ejs               ^1.0.0  →  ^2.0.0
 hexo-renderer-markdown-it-plus  ^1.0.4  →  ^1.0.6
 hexo-server                     ^1.0.0  →  ^3.0.0

之后直接用npm就可以对照更新之后的package.json文件进行新版本的安装

1	npm install

非等间隔时间序列的指数加权移动平均

发表于 2022-12-03

指数加权移动平均（EWMA或EWA）是量化交易中一种简单而强大的工具，特别适用于日内交易。它允许交易者快速轻松地跟踪指定时间段内证券的平均价格，并可用于识别趋势并进行交易决策。

通常来说EWMA的数学公式可以表示为如下：

$\text{EWMA}_{t} = \alpha x_t +(1 - \alpha) \text{EWMA}_{t-1}$

所以其关键在于 $\alpha$ 的计算，在pandas所提供的api中，提供了alpha，halflife，span，com这四个表示不同但是相互等价的参数，通常使用的多为alpha和span。

其中com即为质心（Center of Mass），他的计算，可以认为是针对于每个时间点的权重的加权平均，所找到的位置，即：

$\begin{aligned} \text{CoM} &= \sum_{t=0}^{\infty} (1 - \alpha)^t \alpha t \\ &= \alpha(1 - \alpha)\sum_{t=0}^{\infty} t(1-\alpha)^{t-1} \\ &= \alpha(1 - \alpha) \sum_{t=0}^{\infty} \left[-(1 - \alpha)^t\right]'\\ &= \alpha(1 - \alpha) \left[-\sum_{t=0}^{\infty} (1 - \alpha)^t\right]'\\ &= \alpha(1 - \alpha) \left[ - \frac{1}{\alpha}\right]' \\ &= \frac{1 - \alpha}{\alpha} \end{aligned}$

化简上式，我们可以得到：

$\alpha = 1 / (1 + \text{CoM})$

半衰期（Half-life）即为权重衰减到一半所需要的时间，所以我们可以得到：

$(1 - \alpha)^H = 0.5 \Rightarrow \alpha = 1 - \exp \left(-\frac{\log2}{H}\right)$

以上均为时间间隔等长的情况，当面对不同间隔的时间序列的时候，我们可以使用index参数来指定时间序列的时间间隔，这样可以使得计算的结果更加准确。假设两个时间戳的间隔为dt，那么我们可以使用如下的公式来计算alpha：

$\alpha' = 1 - \exp(-\alpha \text{d}t) \approx 1 - (1 - \alpha \text{d}t) = \alpha \text{d}t$

当时间间隔总是为1的时候，实际上和最开始的公式基本等价。

考虑一个情形，依次有三个时间戳，分别为t0，t1，t2，那么dt1和dt2分别为t1 - t0和t2 - t1，那么我们可以使用如下的公式来计算alpha：

$\begin{aligned} \text{EWMA}_2 &= \alpha_2 x_2 + (1 - \alpha_2) \text{EWMA}_1 \\ &= \alpha_2 x_2 + (1 - \alpha_2) \left(\alpha_1 x_1 + (1 - \alpha_1) \text{EWMA}_0\right) \\ &= \alpha_2 x_2 + \alpha_1(1 - \alpha_2) x_1 + (1 - \alpha_1)(1 - \alpha_2) \text{EWMA}_0 \end{aligned}$

其中t0时刻的权重为：

$(1 - \alpha_1)(1 - \alpha_2) = \exp(-\alpha \text{d}t_1 - \alpha \text{d}t_2) = \exp(-\alpha (t_2 - t_0))$

这样即使当中有多个时间戳到达，对于同样间隔的数据点，其权重仍然一致。对应的python代码如下所示：

from typing import Optional

import numpy as np


class EWMA(object):
    def __init__(
        self,
        com: Optional[float] = None,
        span: Optional[float] = None,
        halflife: Optional[float] = None,
        alpha: Optional[float] = None,
    ) -> None:
        assert (
            (com is None) + (span is None) + (halflife is None) + (alpha is None)
        ) == 3, "only one of com, span, halflife, alpha should be not None"
        if com is not None:
            self.alpha = 1 / (1 + com)
        elif span is not None:
            self.alpha = 2 / (span + 1)
        elif halflife is not None:
            self.alpha = 1 - np.exp(np.log(0.5) / halflife)
        elif alpha is not None:
            self.alpha = alpha

    def __call__(self, x: np.ndarray, index: Optional[np.ndarray] = None) -> np.ndarray:
        if index is not None:
            alpha = 1 - np.exp(-np.diff(index, prepend=0) * self.alpha)
        else:
            alpha = np.ones_like(x) * self.alpha

        ewma = np.zeros_like(x)
        ewma[0] = x[0]
        for i in range(1, len(x)):
            ewma[i] = alpha[i] * x[i] + (1 - alpha[i]) * ewma[i - 1]
        return ewma

[论文笔记] XGBoost: A Scalable Tree Boosting System

发表于 2022-03-16

梯度提升树

首先考虑梯度提升树，考虑一个有 $n$ 个样本，每个样本有 $m$ 个特征的数据集 $\mathcal{D} = \{(\mathrm{x}_i, y_i)\}$ ，一个集成树模型实际上得到的使用K个具有可加性质的函数，得到的输出对应如下所示：

$\hat{y}_i = \phi(\mathrm{x}_i) = \sum_{k=1}^K f_k(\mathrm{x}_i),\quad f_k \in \mathcal{F}$

对于每一棵树而言，一个输入会被映射到一个对应的叶节点，这个节点上的权重就对应这个输入的结果。在这里目标函数使用被正则化的形式：

$\mathcal{L}(\phi) = \sum_{i}l(\hat y_i, y_i) + \sum_K \Omega(f_k)$

$\text{where} \quad \Omega(f) = \gamma T + \frac12 \lambda \|w\|^2$

其中前半部分 $l$ 代表的是损失函数，用来量化预测值与真实值之间的差距，后者是正则化项，用来控制模型的复杂度，防止过拟合。对于树模型而言，正则化项的第一项控制叶节点的数量，后一项控制每个叶节点的权重。如果去掉正则化项，实际上就是普通的梯度提升树。

在对于第 $t$ 颗树的时候，我们需要优化的目标函数实际上以下式子：

$\mathcal{L}^{(t)} = \sum_{i=1}^n l(y_i, \hat y_i^{(t-1)} + f_t(\mathrm{x}_i)) + \Omega(f_t)$

将损失函数展开到二阶近似：

$\mathcal{L}^{(t)} \approx \sum_{i=1}^n \left[ l(y_i, \hat y_i^{(t-1)}) + g_i f_t(\mathrm{x}_i) + \frac12 h_i f_t^2(\mathrm{x}_i)\right] + \Omega(f_t)$

其中 $\hat y_i^{(t-1)}$ 是前 $t-1$ 颗树的结果，在当前的优化实际上是一个常数，将其移除之后得到 $t$ 步的优化函数为：

$\tilde{\mathcal{L}}^{(t)} = \sum_{i=1}^n \left[ g_i f_t(\mathrm{x}_i) + \frac12 h_i f_t^2(\mathrm{x}_i) \right] + \Omega(f_t)$

定义 $I_j = \{j| q(\mathrm{x}_i) = j\}$ 为叶节点 $j$ 上面对应的样本集，于是可以修改求和形式如下：

$\begin{aligned} \tilde{\mathcal{L}}^{(t)} &= \sum_{i=1}^n \left[ g_i f_t(\mathrm{x}_i) + \frac12 h_i f_t^2(\mathrm{x}_i) \right] + \Omega(f_t) \\ &= \sum_{j=1}^T \sum_{i \in I_j} \left[ g_i f_t(\mathrm{x}_i) + \frac12 h_i f_t^2(\mathrm{x}_i) \right] + \gamma T + \frac12 \lambda \sum_{j=1}^T w_j^2 \\ &= \sum_{j=1}^T \sum_{i \in I_j} \left[ g_i w_j + \frac12 h_i w_j^2 \right] + \gamma T + \frac12 \lambda \sum_{j=1}^T w_j^2 \\ &= \sum_{j=1}^T \left[ \left(\sum_{i \in I_j} g_i\right) w_j + \frac12 \left(\sum_{i \in I_j}h_i + \lambda\right) w_j^2 \right] + \gamma T \end{aligned}$

当对于一个确定的树结构， $\gamma T$ 为常量，前面这一项对应于 $w_j$ 的一个二次表达式，可以得到最优解为：

$w_j^\star = - \frac{\sum_{i \in I_j} g_i}{\sum_{i \in I_j}h_i + \lambda}$

带入可以知道最优的值为：

$\tilde{\mathcal{L}}^{(t)}(q) = - \frac12 \sum_{j=1}^T \frac{(\sum_{i \in I_j} g_i)^2}{\sum_{i \in I_j}h_i + \lambda} + \gamma T$

上式仅仅与树结构 $q$ 有关，所以可以作为一个树结构的度量，越小说明这个树结构越好。由于没有办法穷举所有可能的树结构，所以只能贪心地对于树结构去改进，增添新的分支。假设我们希望把一个节点分离成两个子集 $I_L$ 和 $I_R$ 那么这个分裂会带来的 $\tilde{\mathcal{L}}$ 的减少就是：

$\begin{aligned} \mathcal{L}_{\text{split}} &= \mathcal{L}_{\text{before}} - \mathcal{L}_{\text{after}} \\ &= \frac12 \left[ \frac{(\sum_{i \in I_L} g_i)^2}{\sum_{i \in I_L}h_i + \lambda} + \frac{(\sum_{i \in I_R} g_i)^2}{\sum_{i \in I_R}h_i + \lambda} - \frac{(\sum_{i \in I} g_i)^2}{\sum_{i \in I}h_i + \lambda} \right] - \gamma \end{aligned}$

这个值即为分裂带来的增益，应当越大越好，其中前面一项是因为分裂所带来的提升，后面一项是对于分裂使得模型复杂度增加的惩罚。所以 $\gamma$ 相当于给节点分裂设定了阈值，只有当分裂带来的增益超过这个阈值，才会进行树分裂，起到了剪枝的效果。

节点分裂算法

精确贪心算法

关键问题就是如何找到最优的分裂方案来获得最大的分裂增益，最直观的方法就是进行遍历，只要对于数据所有可能的分裂方式进行一次遍历，就可以从中找到增益最大的分裂方式。为了算法能够执行的更加高效，我们需要在最开始对于数据进行一次排序，这样就只要在有序数据上进行一次遍历就可以了。

近似算法

精确贪心算法由于需要遍历所有的可能，非常消耗时间。并且当数据没有办法全部放进内存的时候，进行精准的贪心算法明显是不可行的，所以需要近似算法。精确贪心算法相当于，对于连续变量当中的所有分隔，都作为分割点的候选。一个很自然的近似算法就是，只从当中选择一个子集作为分割点的候选，就是将连续变量给映射到一个个的桶当中，然后基于这些通的统计信息，来选择分割点。具体算法如下图所示，只需要将每一个桶，作为其中的一个样本来思考就可以了。

那么如何分桶实际上就是近似算法的关键所在，XGBoost的论文当中提出了两种方案：

全局方法（global）：即在最开始的构造时间就进行分桶，并且在整个节点分裂的过程当中，都采用最开始的分桶结果。
- 需要进行更少的分桶操作
局部方法（local）：在每次分裂的时候，都重新进行分桶。
- 每一次都在改进分桶方案，对于更深的树会更好
- 需要更少的候选数量

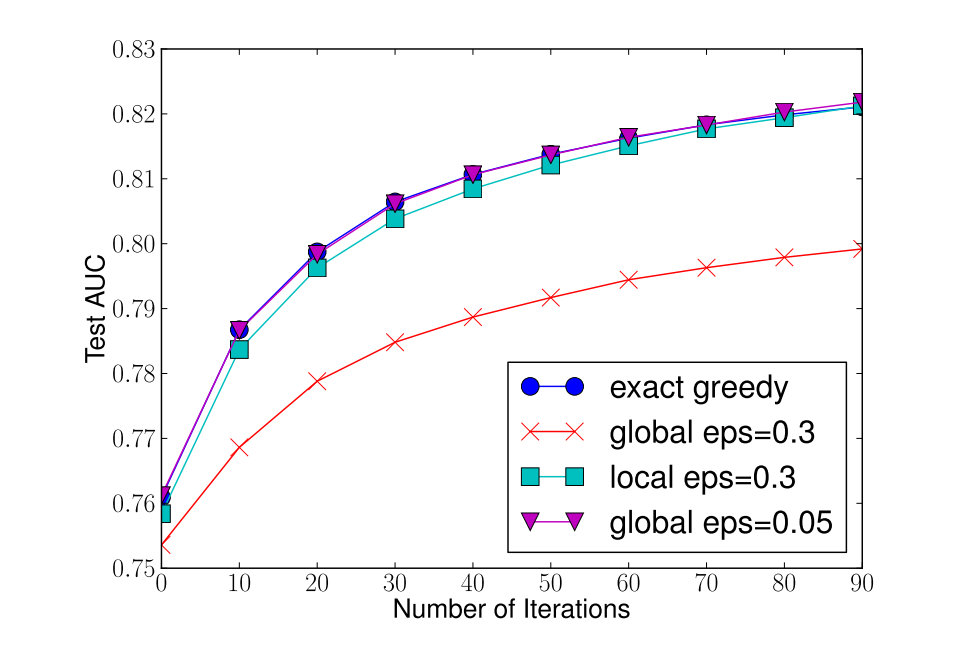
当然从结果上来看，当全局方法的候选数量提升之后，也同样可以获取和局部方法差不多的表现。

对于具体如何选择分割点，论文提出了一个叫做Weighted Quantile Sketch的方法。使用 $\mathcal{D}_k = \{(x_{1k}, h_1), (x_{2k}, h_2) ,\ldots, (x_{nk}, h_n)\}$ 来表示第 $k$ 个特征以及样本的二阶梯度，定义一个rank函数为 $r_k: \mathbb{R} \rightarrow [0, +\infty)$ 如下所示：

$r_k(z) = \frac{1}{\sum_{(x, h) \in \mathcal{D}_k} h} \sum_{(x, h) \in \mathcal{D}_k, x<z}h$

对于之前算法当中所提到的 $\epsilon$ ，实际上就是要找到一系列的分割点 $\{s_{k1}, s_{k_2}, \ldots , s_{kl}\}$ ，使得：

$|r_k({s_{k, j}}) - r_k (s_{k, j+1})| < \epsilon$

所以 $\epsilon$ 相当于一个度量采样点数量的值， $\epsilon$ 越小，对应的分割点就越多，数量近似为 $1 / \epsilon$ 。而采用二阶梯度作为分割依据的根据，来源于之前的目标函数：

$\begin{aligned} \tilde{\mathcal{L}}^{(t)} &= \sum_{i=1}^n \left[ g_i f_t(\mathrm{x}_i) + \frac12 h_i f_t^2(\mathrm{x}_i) \right] + \Omega(f_t) \\ &= \sum_{i=1}^n \frac 12 h_i \left(f_t(\mathrm{x}_i) - \frac{g_i}{h_i}\right)^2 + \Omega(f_t) + \text{constant} \end{aligned}$

之前的目标函数，实际上可以看作是一个以 $h_i$ 为权重的加权平方损失，所以采用 $h_i$ 来计算分割点。对于Weighted Quantile Sketch的具体实现，论文提供了一种新的数据结构，具体在论文附录当中，有兴趣的读者可以自己查看。

XGBoost对于稀疏特征有特殊的优化。稀疏矩阵的产生原因可能是缺失值，又或者One-Hot方法的使用。对于稀疏数据可以做一些特殊处理，我们可以将随意地分到左子树或者右子树，或者可以从数据当中来确定子树的分配方式。

如上述算法所示，只对于对应特征没有缺失值的样本来考虑分割点，而对于所有缺失值，考虑统一分到左边或者统一分到右边。对于两种情况以及所有分割点，取当中能够获得最大增益的作为最终选择的节点分裂方式。

如何阅读一篇论文

发表于 2022-03-14

在B站上看到李沐在做AI方面论文的带读，看了一遍讲如何读论文，做个笔记，顺便记录一些自己的想法。

从整体上来看，整个视频基本上可以用下面这一个表来概括：

	Pass1	Pass2	Pass3
Title	√		√
Abstruction	√		√
Introduction			√
Method		√	√
Experiment		√	√
Conclusion	√		√

Pass1
- 只看标题、摘要和结论
- 观察和自己的研究方向有没有关联性，适不适合自己的研究方向，确定论文值不值得读
Pass2
- 快速过一遍整个论文，不需要了解所有的细节
- 关注重要的图和表，看明白Method当中的流程图以及Experimet中图表的对应指标
- 关注重要的相关工作，如果文章太难，可以先读引用的文献
Pass3
- 关注所有细节
- 换位思考，体会从提出问题到解决问题的全部过程
- 寻找之后可能的改进空间

个人观点：

李沐所讲的论文阅读方法，更多的是针对于经典论文，知道这是一篇好论文之后该如何去读。事实上，AI论文数量激增，大量论文并不能够提供三遍阅读的知识量。更多的是在第二遍阅读的过程当中，关注提出工作的启发点，以及论文当中是否出现类似数据泄露，对比不公平这样的情况。

[Trick] PyTorch Tensor索引子矩阵

发表于 2022-02-22

PyTorch的Tensor支持非常多的索引方法，从Tensor当中取出一个子矩阵是一个常用的需求，如果是需要取出一个连续子矩阵或者子矩阵的索引是等间距排列的情况，可以直接采用切片索引的方式进行解决。对于更一般的情况，没有特别直接的解决办法。

为方便起见，这里定义数据以及需要取出的子矩阵的行列索引如下，这里设置的索引的行列编号相同。

>>> data = torch.arange(36).reshape(6, 6)
>>> data
tensor([[ 0,  1,  2,  3,  4,  5],
        [ 6,  7,  8,  9, 10, 11],
        [12, 13, 14, 15, 16, 17],
        [18, 19, 20, 21, 22, 23],
        [24, 25, 26, 27, 28, 29],
        [30, 31, 32, 33, 34, 35]])
>>> idx = torch.LongTensor([1, 4, 5])
>>> idx
tensor([1, 4, 5])

如果直接利用索引进行取值操作，取到的是对角线上的元素

1 2	>>> data[idx, idx] tensor([ 7, 28, 35])

如果按照先行后列的方法进行取值，可以获得预期的元素，如下所示

>>> data[idx][:, idx]
tensor([[ 7, 10, 11],
        [25, 28, 29],
        [31, 34, 35]])

但是这样取出来的Tensor并不对应原始矩阵当中的子矩阵，而是一个复制，如果在上面进行赋值操作，并不会对原始Tensor进行修改

>>> data[idx][:, idx] = 0
>>> data[idx][:, idx]
tensor([[ 7, 10, 11],
        [25, 28, 29],
        [31, 34, 35]])

如果有修改的需求，更加优雅的方式是采用np.ix_方法或torch.meshgrid方法。

np.ix_的示例如下所示：

>>> data[np.ix_(idx, idx)]
tensor([[ 7, 10, 11],
        [25, 28, 29],
        [31, 34, 35]])
>>> data[np.ix_(idx, idx)] = 0
>>> data
tensor([[ 0,  1,  2,  3,  4,  5],
        [ 6,  0,  8,  9,  0,  0],
        [12, 13, 14, 15, 16, 17],
        [18, 19, 20, 21, 22, 23],
        [24,  0, 26, 27,  0,  0],
        [30,  0, 32, 33,  0,  0]])

torch.meshgrid的示例如下所示：

>>> x, y = torch.meshgrid(idx, idx)
>>> data[x, y]
tensor([[ 7, 10, 11],
        [25, 28, 29],
        [31, 34, 35]])
>>> data[x, y] = 0
>>> data
tensor([[ 0,  1,  2,  3,  4,  5],
        [ 6,  0,  8,  9,  0,  0],
        [12, 13, 14, 15, 16, 17],
        [18, 19, 20, 21, 22, 23],
        [24,  0, 26, 27,  0,  0],
        [30,  0, 32, 33,  0,  0]])

Visual Studio Code配置指南

发表于 2022-02-18

VSCode作为一个轻量级、跨平台的代码编辑器，在各种插件的支持下可以达到媲美IDE的编程开发体验。可以让人在一个编辑器中完成各种编程语言的开发工作，并且支持远程开发和协同开发。这里记录一些个人关于VSCode的基本设置，便于快速的在一台新的机器上配置好VSCode，并且满足基本的编程需求。相关的插件和配置列表可能会随着时间列表不断进行更新。

外观

字体

JetBrains Mono

通过官方下载地址进行下载安装

setting.json 中添加

{
  "editor.fontFamily": "JetBrains Mono",
  "terminal.integrated.fontFamily": "JetBrains Mono"
}

Font Switcher
- 拓展商店安装

颜色主题

One Dark Pro
- 拓展商店安装
file-icons
- 拓展商店安装
Bracket Pair Colorizer
- 拓展商店安装
Chinese (Simplified) (简体中文) Language Pack for Visual Studio Code
- 拓展商店安装
- 为VSCode页面提供中文支持
Better Comments
- 拓展商店安装
- 为注释提供更加丰富的颜色分类
Ruler
- setting.json中添加
  1
  2
  3
  {
  "editor.rulers":[80]
  }
- 在80个字符的位置提供一条标尺

远程开发

Remote -SSH
- 拓展商店安装

编程相关

Code Runner
- 拓展商店安装

Python

Python Extension Pack
- 拓展商店安装
Mypy
- 拓展商店安装
- 为Python提供静态类型检查

Black

setting.json中添加

{
  "python.formatting.provider": "black",
  "editor.formatOnSave": true,
}

为Python提供代码格式化

辅助编程

GitHub Copilot
- 拓展商店安装
- 需要绑定GitHub账号

其他

LeetCode
- 拓展商店安装
Docker
- 拓展商店安装
Kubernetes
- 拓展商店安装