Goodbye 2019

发表于 2019-12-31

2019

无所得

有所失

Variational Inference

发表于 2019-12-28

先回顾一下全贝叶斯推断：

训练阶段：

$p(\theta|X_{tr},Y_{tr}) =\frac{p(Y_{tr}|X_{tr},\theta)p(\theta)}{\color{red}{\int p(Y_{tr}|X_{tr},\theta)p(\theta) d\theta}}$

测试阶段：

$p(y|x,X_{tr},Y_{tr}) =\color{red}{\int p(y|x,\theta) p(\theta|X_{tr},Y_{tr})d\theta }$

红色分布难以计算，使得后验分布只有在面对简单的共轭模型才能被精确求解

Approximate inference

概率模型： $p(x,\theta)=p(x|\theta)p(\theta)$

变分推断（Variational Inference）：

采用一个简单的分布来近似后验： $p(\theta|x)\approx q(\theta)\in \mathcal{Q}$

有偏的
高效并且可拓展

蒙特卡洛方法（MCMC）：

从没有标准化的 $p(\theta|x)$ 里面进行采样（因为下面归一化的部分难以计算）：

无偏的
需要很多的采样才能近似

Variational inference

$\begin{aligned} \log p(x) &= \int q(\theta)\log p(x) d\theta =\int q(\theta)\log \frac{p(x,\theta)}{p(\theta|x)}d\theta\\ &=\int q(\theta)\log \frac{p(x,\theta)q(\theta)}{p(\theta|x)q(\theta)}d\theta\\ &=\int q(\theta)\log \frac{p(x,\theta)}{q(\theta)}d\theta + \int q(\theta)\log\frac{q(\theta)}{p(\theta|x)}d\theta\\ &=\color{green}{\mathcal{L}(q(\theta))}+ \color{red}{KL(q(\theta)||p(\theta|x))} \end{aligned}$

前面的绿色部分是ELBO(Evidence lower bound)

后面的红色部分是用于变分推断的KL散度，KL散度越小，说明我们的估计与后验分布越接近

但是后验分布是未知的，否则就不需要求解了，再看一遍上面这个公式：

$\log p(x) = \mathcal{L}(q(\theta)) + KL(q(\theta)||p(\theta|x))$

可以发现前面 $\log p(x)$ 与 $q(\theta)$ 是没有关系的，那么要最小化KL散度，实际上就相当于最大化ELBO：

$KL(q(\theta)||p(\theta|x))\rightarrow\min_{q(\theta)\in \mathcal{Q}} \quad \Leftrightarrow \quad \mathcal{L}(q(\theta))\rightarrow\max_{q(\theta)\in\mathcal{Q}}$

改写一遍变分下界：

$\begin{aligned}\mathcal{L}(q(\theta))&=\int q(\theta)\log\frac{p(x,\theta)}{q(\theta)}d\theta\\ &=\int q(\theta)\log\frac{p(x|\theta)p(\theta)}{q(\theta)}d\theta\\ &= \color{green}{\mathbb{E}_{q(\theta)}\log p(x|\theta) } - \color{red}{KL(q(\theta)||p(\theta))} \end{aligned}$

前面绿色的为数据项，后面红色的为正则项

最终的优化问题就在于：

$\mathcal{L}(q(\theta)) = \int q(\theta) \log \frac{p(x,\theta)}{q(\theta)}d\theta \quad \rightarrow \quad \max_{q(\theta)\in \mathcal{Q}}$

问题的关键是，怎么对于一个概率分布进行最优化

Mean Field Variational Inference

Mean Field Approximation

$\mathcal{L}(q(\theta)) = \int q(\theta)\log \frac{p(x,\theta)}{q(\theta)}d\theta \quad \rightarrow \quad \max_{q(\theta)=q_1(\theta_1)\cdot \ldots \cdot q_m(\theta_m)}$

块坐标上升法（Block coordinate assent）:

每次都固定除了一个维度分布其他的部分 $\{q_i(\theta_i)\}_{i\ne j}$ ，然后对一个维度上的分布进行优化

$\mathcal{L}(q(\theta)) \quad \rightarrow \quad \max_{q_j(\theta_j)}$

由于除了 $q_j(\theta_j)$ 其他维度都是固定的，可以得到如下的数学推导：

$\begin{aligned} \mathcal{L}(q(\theta)) &=\int q(\theta)\log \frac{p(x,\theta)}{q(\theta)}\\ &=\mathbb{E}_{q(\theta)}\log p(x,\theta) - \mathbb{E}_{q(\theta)}\log q(\theta)\\ &=\mathbb{E}_{q(\theta)}\log p(x,\theta) - \sum_{k=1}^m \mathbb{E}_{q_k(\theta_k)}\log q_k(\theta_k)\\ &=\mathbb{E}_{q_j(\theta_j)}\left[\mathbb{E}_{q_{i\ne j}}\log p(x,\theta)\right] - \mathbb{E}_{q_j(\theta_j)}\log q_j(\theta_j)+Const\\ &\left\{r_j(\theta_j) = \frac{1}{Z_j} \exp\left(\mathbb{E}_{q_{i\ne j}}\log p(x,\theta)\right)\right\}\\ &=\mathbb{E}_{q_j(\theta_j)} \log \frac{r_j(\theta_j)}{q_j(\theta_j)}+Const\\ &=-KL\left(q_j(\theta_j)||r_j(\theta_j)\right)+Const \end{aligned}$

在块坐标下降中的每一步优化问题转化为了：

$\mathcal{L}(q(\theta)) = -KL(q_j(\theta_j)||r_j(\theta_j)) + Const \quad \rightarrow \quad \max_{q_j(\theta_j)}$

实际上就是要最小化KL散度，容易发现解为：

$q_j(\theta_j) = r_j(\theta_j) =\frac{1}{Z_j} \exp\left(\mathbb{E}_{q_{i\ne j}}\log p(x,\theta)\right)$

Parametric variational inference

考虑对于变分分布的参数族：

$q(\theta) = q(\theta|\lambda)$

限制在于，我们选择了一族固定的分布形式：

如果选择的形式过于简单，我们可能不能有效地建模数据
如果选择的形式足够复杂，我们不能保证把它训得很好来拟合数据

但这样就把变分推断就转变成了一个参数优化问题：

$\mathcal{L}(q(\theta|\lambda)) = \int q(\theta|\lambda) \log\frac{p(x,\theta)}{q(\theta|\lambda)}d\theta \quad \rightarrow \quad \max_{\lambda}$

只要我们能够计算变分下界(ELBO)对于 $\theta$ 的导数，那么就可以使用数值优化方法来对这个优化问题进行求解

Summary

Full Bayesian inference	$p(\theta\mid x)$
MP inference	$p(\theta\mid x)\approx\delta(\theta-\theta_{MP})$
Mean field variational inference	$p(\theta\mid x)\approx q(\theta)=\prod_{j=1}^m q_j(\theta_j)$
Parametric variational inference	$p(\theta\mid x)\approx q(\theta)=q(\theta\mid\lambda)$

Bayesian Framework

发表于 2019-12-28

$\text{Conditional} = \frac{\text{Joint}}{\text{Marginal}},\quad p(x|y)=\frac{p(x,y)}{p(y)}$

Product Rule

联合分布可以被表示为一维的条件分布的乘积

$p(x,y,z)=p(x|y,z)p(y|z)p(z)$

Sum Rule

任何边缘分布可以利用联合分布通过积分得到

$p(y) = \int p(x,y)dx$

Bayes理论

$p(y|x) = \frac{p(x,y)}{p(x)} = \frac{p(x|y)p(y)}{p(x)}=\frac{p(x|y)p(y)}{\int p(x|y)p(y)dy}$

Bayes理论定义了当新的信息到来的时候，可能性的改变：

$\text{Posterior} = \frac{\text{Likelihood} \times \text{Prior}}{\text{Evidence}}$

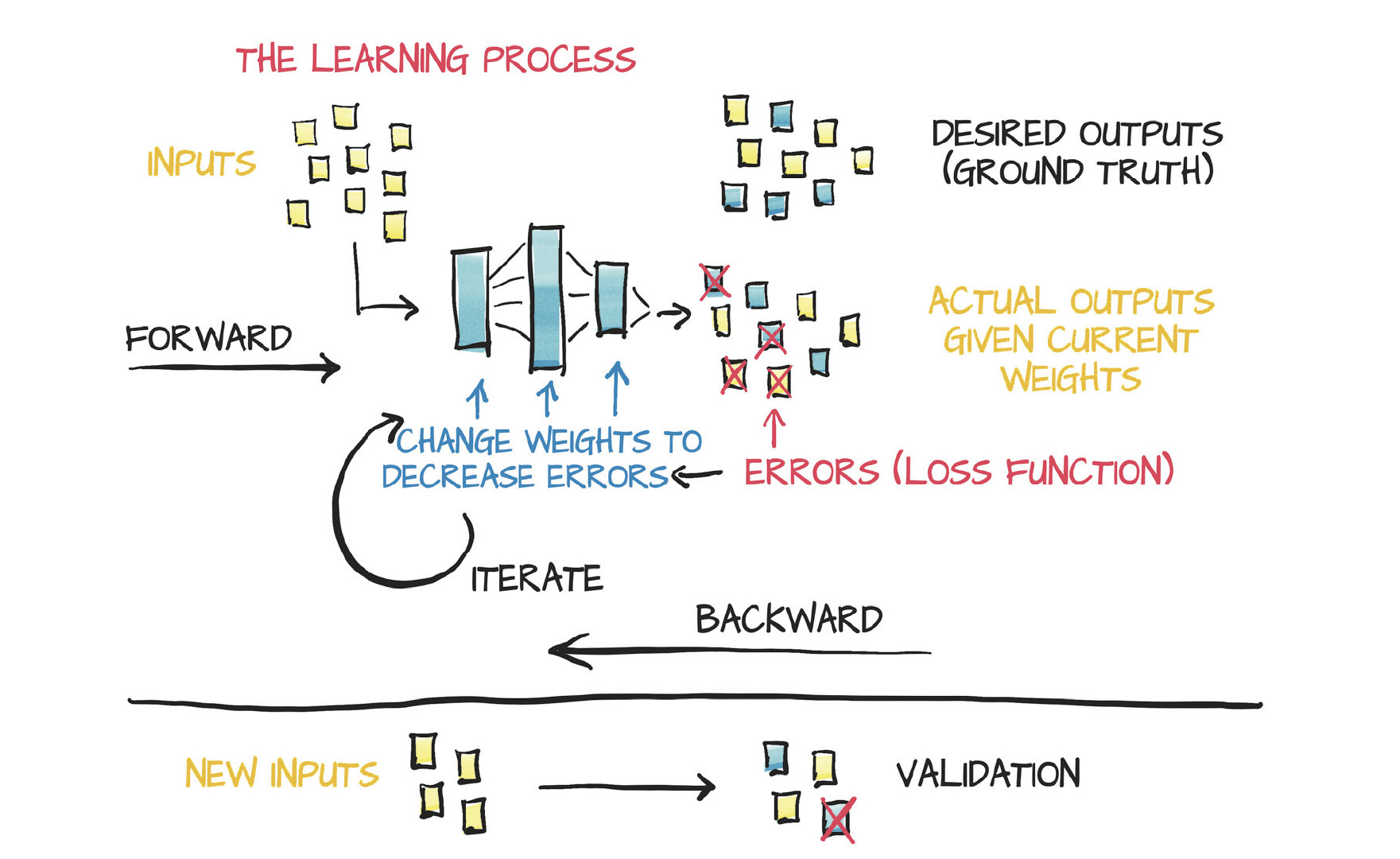
统计推断（Statistical inference）

问题描述：

给定从分布 $p(x|\theta)$ 中得到的独立同分布变量 $X = (x_1,\ldots,x_n)$ ，来估计 $\theta$

常规方法：

采用极大似然估计（maximum likelihood estimation）

$\theta_{ML} = \arg \max p(X|\theta) = \arg \max \prod_{i=1}^{n}p(x_i|\theta) = \arg \max \sum_{i=1}^{n} = \log p(x_i|\theta)$

贝叶斯方法：

用先验 $p(\theta)$ 来编码 $\theta$ 的不确定性，然后采用贝叶斯推断

$p(\theta|X) = \frac{\prod_{i=1}^{n}p(x_i|\theta)p(\theta)} {\int \prod_{i=1}^{n}p(x_i|\theta)p(\theta)d\theta}$

频率学派vs. 贝叶斯学派

	频率学派	贝叶斯学派
变量	有随机变量也有确定的	全都是随机变量
适用范围	$n>>d$	$\forall n$

现代机器学习模型中可训练的参数数量已经接近训练数据的大小了
频率学派得到的结果实际上是一种受限制的Bayesian方法：

$\lim_{n/d \rightarrow \infty}p(\theta|x_1,\ldots,x_n)=\delta(\theta-\theta_{ML})$

注：此处的 $\delta$ 函数指的是狄拉克函数

贝叶斯方法的优点

可以用先验分布来编码我们的先验知识或者是希望的做种结果
先验是一种正则化的方式
相对于 $\theta$ 的点估计方法，后验还包含有关于估计的不确定性关系的信息

概率机器学习模型

数据：

$x$ – 观察到变量的集合（features）
$y$ – 隐变量的集合（class label / hidden representation, etc.)

模型：

$\theta$ – 模型的参数（weights）

Discriminative probabilistic ML model

通常假设 $\theta$ 的先验与 $x$ 没有关系

$p(y,\theta|x) = p(y|x,\theta)p(\theta)$

Examples:

分类或者回归任务（隐层表示比观测空间简单得多）
机器翻译（隐层表示和观测的空间有着相同的复杂度）

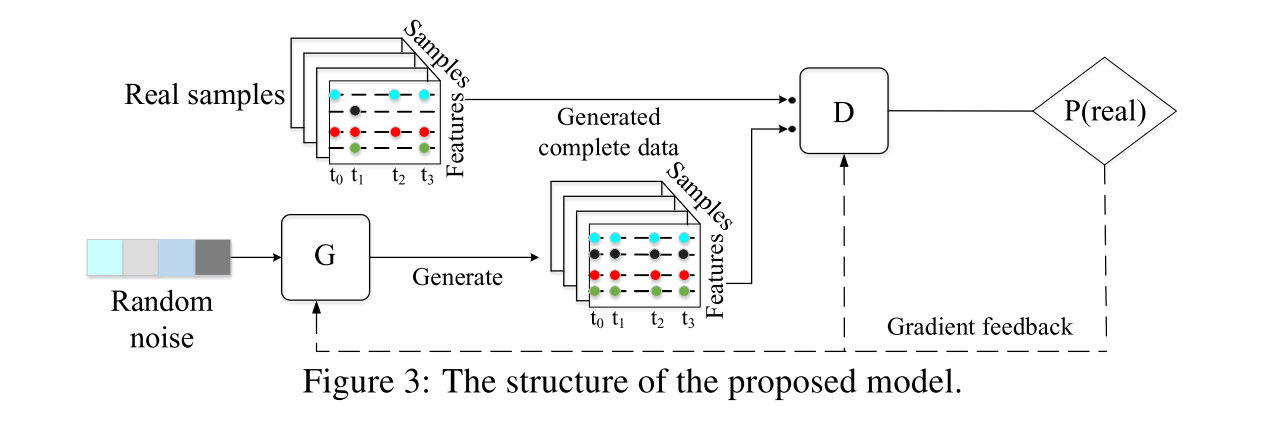
Generative probabilistic ML model

可能会很难训练，因为通常而言观测到的 $x$ 会比隐层复杂很多。

Examples：

文本，图片的生成

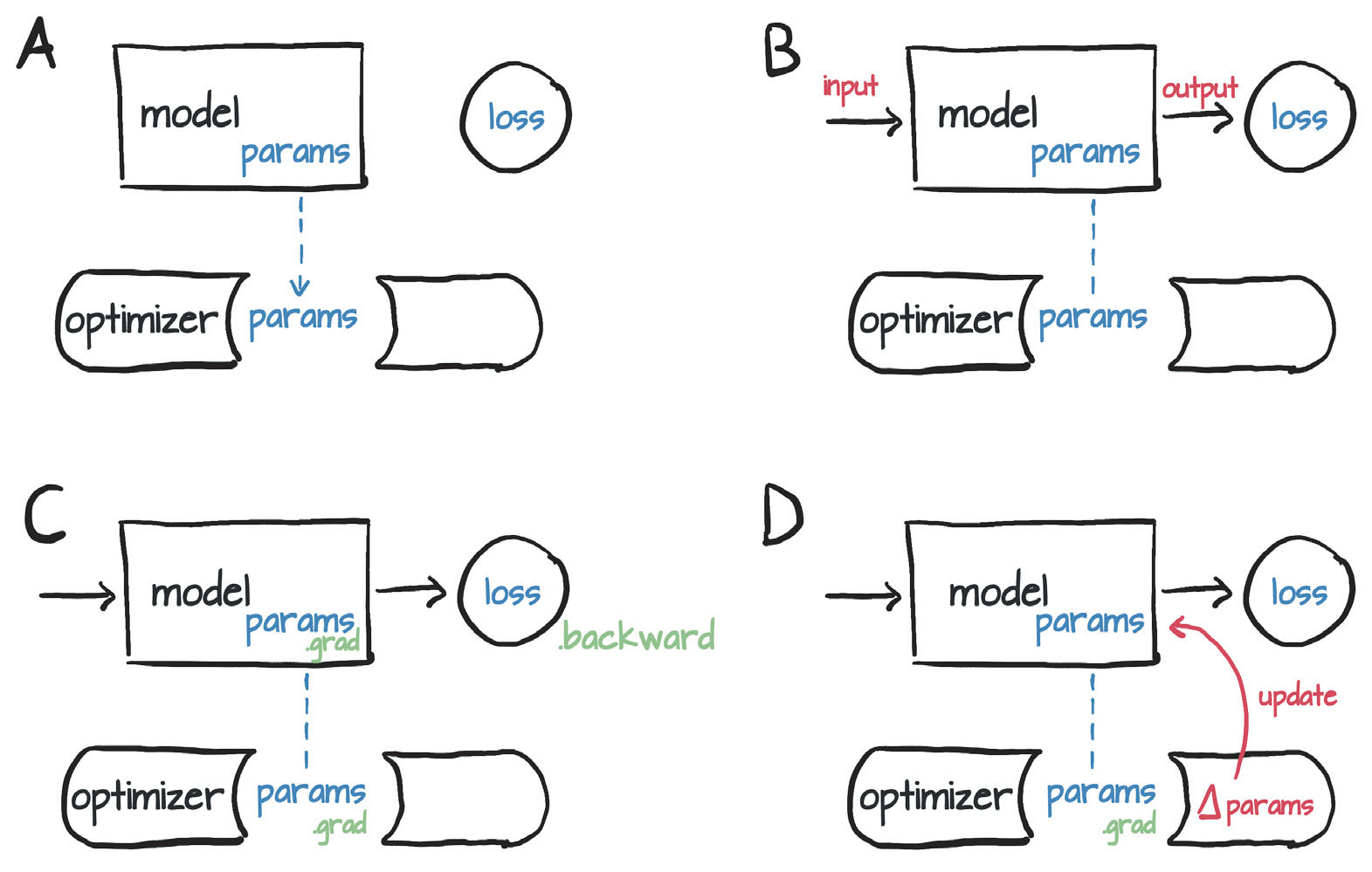
贝叶斯机器学习模型的训练与预测

Training阶段： $\theta$ 上的贝叶斯推断

$p(\theta|X_{tr},Y_{tr}) = \frac{p(Y_{tr}|X_{tr},\theta)p(\theta)} {\int p(Y_{tr}|X_{tr},\theta)p(\theta) d\theta}$

结果：采用 $p(\theta)$ 分布比仅仅采用一个 $\theta_{ML}$ 有着更好地效果

模型融合总是比一个最优模型的效果更好
后验分布里面含有所有从训练数据中学到的相关内容，并且可以模型提取用于计算新的后验分布

Testing阶段：

从training中我们得到了后验分布 $p(\theta|X_{tr},Y_{tr})$
获得了新的的数据点 $x$
需要计算对于 $y$ 的预测

$p(y|x,X_{tr},Y_{tr}) = \int p(y|x,\theta) p(\theta|X_{tr},Y_{tr})d\theta$

重新看一遍

训练阶段：

$p(\theta|X_{tr},Y_{tr}) =\frac{p(Y_{tr}|X_{tr},\theta)p(\theta)}{\color{red}{\int p(Y_{tr}|X_{tr},\theta)p(\theta) d\theta}}$

测试阶段：

$p(y|x,X_{tr},Y_{tr}) =\color{red}{\int p(y|x,\theta) p(\theta|X_{tr},Y_{tr})d\theta }$

红色部分的内容通常是难以计算的！

共轭分布

我们说分布 $p(y)$ 和 $p(x|y)$ 是共轭的当且仅当 $p(y|x)$ 和 $p(y)$ 是同类的，即后验分布和先验分布同类。

$p(y)\in \mathcal A(\alpha),\quad p(x|y)\in \mathcal B(\beta)\quad \Rightarrow \quad p(y|x)\in \mathcal A(\alpha^{\prime})$

Intuition:

$p(y|x) = \frac{p(x|y)p(y)}{\int p(x|y)p(y)dy}\propto p(x|y)p(y)$

由于任何 $\mathcal A$ 中的分布是归一化的，分母是可计算的
我们需要做的就是计算 $\alpha^{\prime}$

这种情况下贝叶斯推断可以得到闭式解！

常见的共轭分布如下表：

Likelihood $p(x\mid y)$	$y$	Conjugate prior $p(y)$
Gaussian	$\mu$	Gaussian
Gaussian	$\sigma^{-2}$	Gamma
Gaussian	$(\mu,\sigma^{-2})$	Gaussian-Gamma
Multivariate Gaussian	$\Sigma^{-1}$	Wishart
Bernoulli	$p$	Beta
Multinomial	$(p_1,\ldots,p_m)$	Dirichlet
Poisson	$\lambda$	Gamma
Uniform	$\theta$	Pareto

举个例子：丢硬币

我们有一枚可能是不知道是否均匀的硬币
任务是预测正面朝上的概率 $\theta$
数据： $X=(x_1,\ldots,x_n)$ ， $x\in\{0,1\}$

概率模型如下：

$p(x,\theta) = p(x|\theta)p(\theta)$

其中对于 $p(x|\theta)$ 的似然为：

$Bern(x|\theta) = \theta^x(1-\theta)^{1-x}$

但是不知道 $p(\theta)$ 的先验是多少

怎样选择先验概率分布？

正确的定义域： $\theta \in [0,1]$
包含先验知识：一枚硬币是均匀的可能性非常大
推断复杂度的考虑：使用共轭先验

Beta分布是满足所有条件的！

$Beta(\theta|a,b) = \frac{1}{\mathrm{B}(a,b)}\theta^{a-1}(1-\theta)^{b-1}$

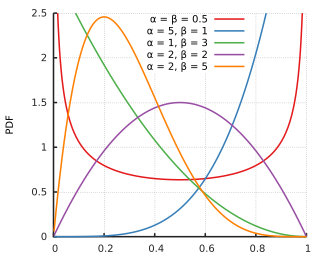
同样也适用于大部分不均匀硬币的情况

让我们来检验似然和先验是不是共轭分布：

$p(x|\theta)=\theta^x(1-\theta)^{1-x}\qquad p(\theta) = \frac{1}{\mathrm{B}(a,b)}\theta^{a-1}(1-\theta)^{b-1}$

方法——检验先验和后验是不是在同样的参数族里面

$\begin{aligned} p(\theta)&=C\theta^{\alpha}(1-\theta)^{\beta}\\ p(\theta|x)&=C^{\prime}p(x|\theta)p(\theta)\\ &=C^{\prime}\theta^x(1-\theta)^{1-x}\frac{1}{\mathrm{B}(a,b)}\theta^{a-1}(1-\theta)^{b-1}\\ &=\frac{C^{\prime}}{\mathrm{B}(a,b)}\theta^{x+a-1}(1-\theta)^{b-x}\\ &=C^{\prime\prime}\theta^{\alpha^{\prime}}(1-\theta)^{\beta^{\prime}} \end{aligned}$

由于先验和后验形式相同，所以确实是共轭的！

现在考虑接收到数据之后的贝叶斯推断：

$\begin{aligned} p(\theta|X) &= \frac{1}{Z}p(X|\theta)p(\theta)\\ &= \frac{1}{Z}p(\theta)\prod_{i=1}^{n} p(x_i|\theta) \\ &=\frac{1}{Z} \frac{1}{\mathrm{B}(a,b)}\theta^{a-1}(1-\theta)^{b-1} \prod_{i=1}^{n} \theta^{x_i}(1-\theta)^{1-x_i}\\ &=\frac{1}{Z^{\prime}}\theta^{a+\sum_{i=1}^n x_i -1}(1-\theta)^{b+n-\sum_{i=1}^n-1}\\ &=\frac{1}{Z^{\prime}}\theta^{a^\prime -1}(1-\theta)^{b^\prime -1} \end{aligned}$

新的参数为：

$a^\prime = a+\sum_{i=1}^nx_i \qquad b^{\prime}=b+n-\sum_{i=1}^nx_i$

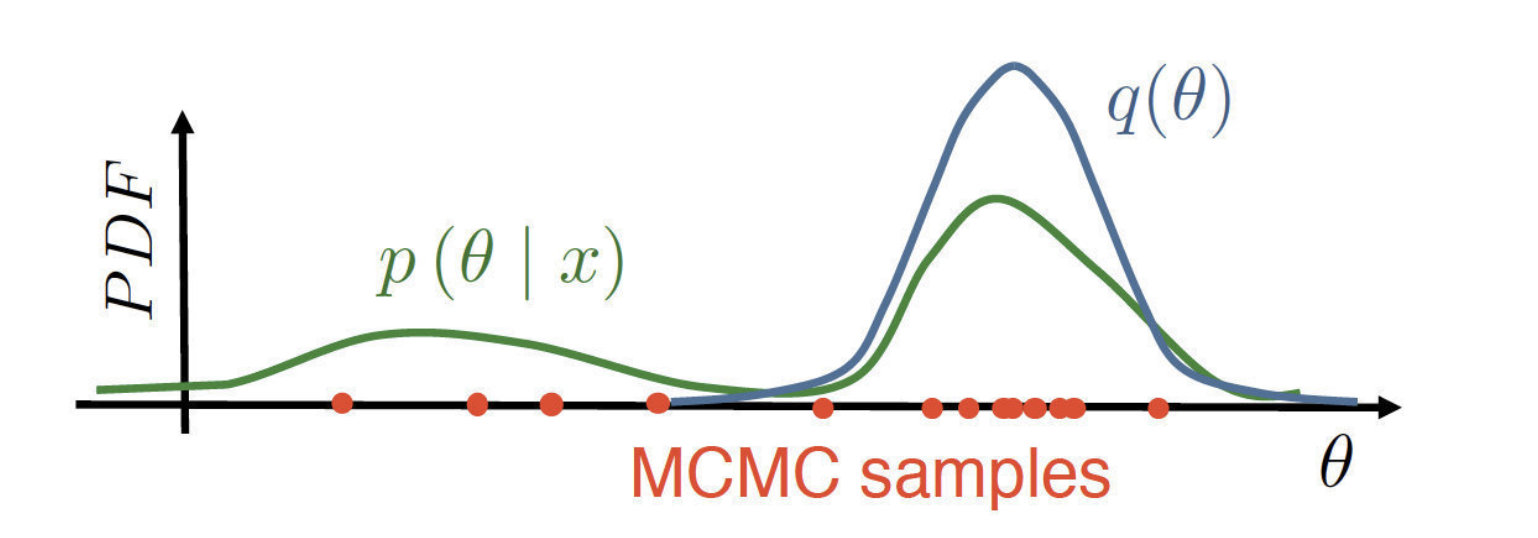
那么问题来了，当没有共轭分布的时候我们应该怎么做？

最简单的方法：选择可能性最高的参数

训练阶段：

$\theta_{MP}=\arg \max p(\theta|X_{tr},Y_{tr}) = \arg \max p(Y_{tr}|X_{tr},\theta)p(\theta)$

测试阶段：

$p(y|x,X_{tr},Y_{tr}) = \int p(y|x,\theta)p(\theta,X_{tr},Y_{tr})d\theta \approx p(y|x,\theta_{MP})$

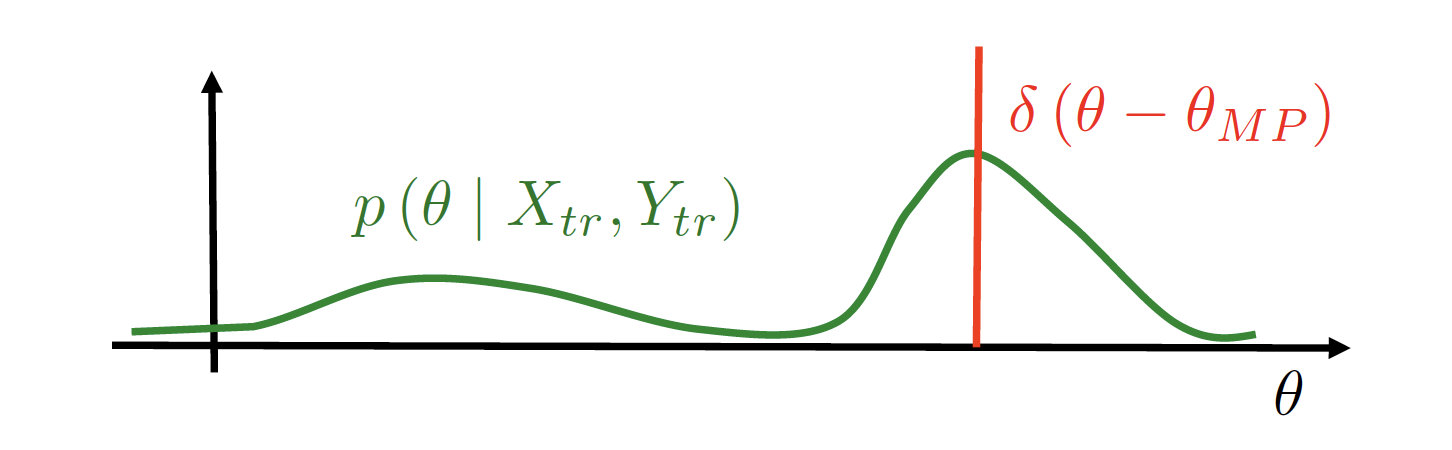
这种情况下我们并不能计算出正确的后验。

[论文笔记] Multivariate Time Series Imputation with Generative Adversarial Networks

发表于 2019-12-15

基本介绍

传统处理数据集中缺失值一般有两种方法：

直接针对缺失值进行建模
- 对于每个数据集，需要单独建模
对于缺失值进行填充得到完整数据集，再用常规方法进行分析
- 删除法，会丢失到一些重要信息，缺失率越高，情况越严重
- 用均值/中位数/众数填充，没有利用现有的其他信息
- 基于机器学习的填充方法
  - EM
  - KNN
  - Matrix Factorization

考虑一个这样的数据，时间序列 $X$ 是 $T=(t_0, \ldots, t_{n-1})$ 的一个观测， $X=\left(x_{t_{0}}, \ldots, x_{t_{i}}, \ldots, x_{t_{n-1}}\right)^{\top} \in \mathbb{R}^{n \times d}$ ，例如：

$X=\left[\begin{array}{cccc}{1} & {6} & {\text { none }} & {9} \\ {7} & {\text { none }} & {7} & {\text { none }} \\ {9} & {\text { none }} & {\text { none }} & {79}\end{array}\right], T=\left[\begin{array}{c}{0} \\ {5} \\ {13}\end{array}\right]$

利用mask矩阵 $M\in \mathbb{R}^{n \times d}$ 来表示 $X$ 中的值存在与否，如果存在， $M^{j}_{t_i}=1$ 否则的话 $M^{j}_{t_i}=0$ 。

总体的基本框架如下，generator从随机的输入中生成时间序列数据，discriminator尝试判别是真的数据还是生成的假数据，通过bp进行优化：

GAN框架

由于最初始的GAN容易导致模型坍塌的问题，采用WGAN（利用Wasserstein距离），他的loss如下：

$\begin{array}{c}{L_{G}=\mathbb{E}_{z \sim P_{g}}[-D(G(z))]} \\ {L_{D}=\mathbb{E}_{z \sim P_{g}}[D(G(z))]-\mathbb{E}_{x \sim P_{r}}[D(x)]}\end{array}$

采用基于GRU的GRUI单元作为G和D的基本网络，来缓解时间间隔不同所带来的的问题。可以知道的是，老的观测值所带来的影响随着时间的推移应当更弱，因为他的观测值已经有了一段时间的缺失。

时间衰减（time decay)

采用一个time lag矩阵 $\delta\in \mathbb{R}^{n\times d}$ 来表示当前值和上一个有效值之间的时间间隔。

$\delta_{t_{i}}^{j}=\left\{\begin{array}{ll}{t_{i}-t_{i-1},} & {M_{t_{i-1}}^{j}==1} \\ {\delta_{t_{i-1}}^{j}+t_{i}-t_{i-1},} & {M_{t_{i-1}}^{j}==0 \& i>0} \\ {0,} & {i==0}\end{array} \quad ; \quad \delta=\left[\begin{array}{cccc}{0} & {0} & {0} & {0} \\ {5} & {5} & {5} & {5} \\ {8} & {13} & {8} & {13}\end{array}\right]\right.$

利用一个时间衰减向量 $\beta$ 来控制过去观测值的影响，每一个值都应当是在 $(0,1]$ 的，并且可以知道的是， $\delta$ 中的值越大， $\beta$ 中对应的值应当越小，其中 $W_{\beta}$ 更希望是一个完全的矩阵而不是对角阵。

$\beta_{t_i} = 1/ e^{\max(0,W_{\beta}\delta_{t_i}+b_{\beta})}$

GRUI

GRUI的更新过程如下：

$\begin{aligned}h_{t_{i-1}}^{\prime}&=\beta_{t_{i}} \odot h_{t_{i-1}}\\ \mu_{t_{i}} &= \sigma(W_{\mu}\left[h_{t_{i-1}}^{\prime},x_{t_{i}}\right]+b_{\mu}) \\ r_{t_{i}} &= \sigma(W_{r}\left[h_{t_{i-1}}^{\prime},x_{t_{i}}\right]+b_{r}) \\ \tilde{h}_{t_{i}} &= \tanh(W_{\tilde{h}}\left[r_{t_{i}} \odot h_{t_{i-1}}^{\prime},x_{t_{i}}\right]+b_{\tilde{h}})\\ h_{t_{i}}&=(1-\mu_{t_{i}})\odot h_{t_{i-1}}^{\prime}+\mu_{t_{i}}\odot \tilde{h}_{t_{i}}\end{aligned}$

D和G的结构：

D过一个GRUI层，最后一个单元的隐层表示过一个FC（带dropout）

G用一个GRUI层和一个FC，G是自给的网络（self-feed network），当前的输出会作为下一个迭代的输入。最开始的输入是一个随机噪声。假数据的 $\delta$ 的每一行都是常量。

G和D都采用batch normalization。

缺失值填补方法

考虑到 $x$ 的缺失，可能 $G(z)$ 在 $x$ 没有缺失的几个值上面都表现的非常好，但是却可能和实际的 $x$ 差得很多。

文章中定义了一个两部分组成的loss function来衡量填补的好坏。第一部分叫做masked reconstruction loss，用来衡量和原始不完整的时间序列数据之间的距离远近。第二部分是discriminative loss，让生成的 $G(z)$ 尽可能真实。

Masked Reconstruction Loss

只考虑没有缺失值之间的平方误差

$L_{r}(z)=\|X \odot M-G(z) \odot M\|_{2}$

Discriminative Loss

$L_d(z) = -D(G(z))$

Imputation Loss

$L_{imputation}(z) = L_{r}(z)+\lambda L_{d}(z)$

对于每个原始的时间序列 $x$ ，从高斯分布中采样 $z$ ，通过一个已经训练好的 $G$ 获得 $G(z)$ 。之后通过最小化 $L_{imputation}(z)$ 来进行训练，收敛之后用 $G(z)$ 填充缺失的部分。

$x_{imputed} = M\odot x+(1-M)\odot G(z)$

[读书笔记] Deep Learning with Pytorch -- Chapter 5

发表于 2019-12-13

这一章采用神经网络方法来搭建模型，从而能够解决更为实际的问题。

神经网络单元

一个神经单元可以看做 $o = f(w*x+b)$ ，一个线性的变换再加上一个非线性的激活函数，常见的激活函数如下：

其中ReLU是最为通用的激活函数！

激活函数的通用特征：

非线性
可导（可以存在点不连续，比如Hardtanh和ReLU）
有至少一个敏感的域，输入的变化会改变输出的变化
有至少一个不敏感的域，输入的变化对输出的变化无影响或极其有限
当输入是负无穷的时候有lower bound，当输入是正无穷的时候有upper bound（非必须）

PyTorch中的nn

PyTorch中有一系列构建好的module来帮助构造神经网络，一个module是nn.Module基类派生出来的一个子类。每个Module有一个或多个Parameter对象。一个Module同样可以可以由一个或多个submodules，并且可以同样可以追踪他们的参数。

注意：submodules不能再list或者dict里面。否则的话优化器没有办法定位他们，更新参数。如果要使用submodules的list或者dict，PyTorch提供了nn.ModuleList和nn.ModuleDict。

直接调用nn.Module实际上等同调用了forward方法，理论上调用forward也可以达到同样的效果，但是实际上不应该这么操作。

现在的training loop长这个样子：

def training_loop(n_epochs, optimizer, model, loss_fn, t_u_train, t_u_val, t_c_train, t_c_val):
  for epoch in range(1, n_epochs + 1):
    t_p_train = model(t_u_train)
    loss_train = loss_fn(t_p_train, t_c_train)
    
    t_p_val = model(t_u_val)
    loss_val = loss_fn(t_p_val, t_c_val)
    
    optimizer.zero_grad()
    loss_train.backward()
    optimizer.step()
    
    if epoch == 1 or epoch %1000 == 0:
      print("Epoch {}, Training loss {}, Validation loss {}".format(epoch, float(loss_train), float(loss_val)))

调用方法：

linear_model = nn.Linear(1,1)
optimizer = optim.SGD(linear_model.parameters, lr=1e-2)

training_loop(
	n_epochs = 3000,
	optimizer = optimizer,
	model = linear_model,
	loss_fn = nn.MSELoss(),
	t_u_train = t_un_train,
	t_u_val = t_un_val,
	t_c_train = t_c_train,
	t_c_val = t_c_val)

现在考虑一个稍微复杂一点的情况，一个线性模型套一个激活函数再套一个线性模型，PyTorch提供了nn.Sequential容器：

1
2
3

seq_model = nn.Sequential(nn.Linear(1,13),
                         nn.Tanh(),
                         nn.Linear(13,1))

可以通过model.parameters()来得到里面的参数：

1	[param.shape for param in seq_model.parameters()]

如果一个模型通过很多子模型构成的话，能够通过名字辨别是非常方便的事情，PyTorch提供了named_parameters方法

1 2	for name, param in seq_model.named_parameters(): print(name,param.shape)

Sequential按模块在里面出现的顺序进行排序，从0开始命名。Sequential同样接受OrderedDict，可以在里面对传入Sequential的每个model进行命名

from collections import OrderedDict

seq_model = nn.Seqential(OrderedDict([('hidden_linear',nn.Linear(1,8)),
                                     ('hidden_activation',nn.Tanh()),
                                     ('outpu_linear',nn.Linear(8,1))]))

for name, param in seq_model.named_parameters():
  print(name,param.shape)

同样可以把子模块当做属性来对于特定的参数进行访问：

1	seq_model.output_linear.bias

可以定义nn.Module的子类来更大程度上的自定义：

class SubclassModel(nn.Module):
  def __init__(self):
    super().__init__()
    self.hidden_linear = nn.Linear(1,11)
    self.hidden_activation = nn.Tanh()
    self.output_linear = nn.Linear(11,1)
  
  def forward(self, input):
    hidden_t = self.hidden_linear(input)
    activated_t = self.hidden_activation(hidden_t)
    output_t = self.output_linear(activated_t)
    
    return output_t

subclass_model = SubclassModel()

这样极大提高了自定义能力，可以在forward里面做任何你想做的事情，甚至可以写类似于activated_t = self.hidden_activation(hidden_t) if random.random() >0.5 else hidden_t，由于PyTorch采用的是动态的运算图，所以无论random.random()返回的是什么都可以正常运行。

在subclass内部所定义的module会自动的注册，和named_parameters中类似。nn.ModuleList和nn.ModuleDict也会自动进行注册。

PyTorch中有functional，它代表输出完全由输入决定，像nn.Tanh这种可以直接写在forward里面。

class SubclassFunctionalModel(nn.Module):
  def __init__(self):
    super().__init__()
    
    self.hidden_linear = nn.Linear(1,14)
    
    self.output_linear = nn.Linear(14,1)
  def forward(self, input):
    hidden_t = self.hidden_linear(input)
    activated_t = torch.tanh(hidden_t)
    output_t = self.output_linear(activated_t)
    
    return output_t
func_model = SubclassFunctionalModel()

在PyTorch1.0中有许多函数被放到了torch命名空间中，更多的函数留在torch.nn.functional里面。

[读书笔记] Deep Learning with Pytorch -- Chapter 4

发表于 2019-12-13

开普勒从数据中得到三定律，同样利用的是现在数据科学的思想，他的步骤如下：

得到数据
可视化数据
选择最简单的可能模型来拟合数据
将数据分成两部分，一部分用来推导，另一部分用来检验
从一个奇怪的初始值除法逐渐迭代
在独立的验证集上检验所得到的模型
尝试对模型进行解释

今日的学习方法实际上就是自动寻找适合的函数形式来拟合输入输出，流程如下：

输入测试数据->计算输出->计算误差->反向传播->更新权重

问题示例

一个简单的摄氏度和华氏度转换的方法。

定义model和loss函数：

def model(t_u, w, b):
  return w * t_u + b

def loss_fn(t_p, t_c):
  squared_diffs = (t_p - t_c)**2
  return squared_diffs.mean()

正向过程：

w = torch.ones(1)
b = torch.zeros(1)

t_p = model(t_u, w, b)

loss = loss_fn(t_p, t_c)

采用梯度下降进行反向传播，这里采用最简单的方法进行梯度的模拟计算：

delta = 0.1
learning_rate = 1e-2

loss_rate_of_change_w = (loss_fn(model(t_u, w+delta, b), t_c) - (loss_fn(model, t_u, w-delta, b), t_c)) / (2.0*delta)

loss_rate_of_change_b = (loss_fn(model(t_u, w, b+delta), t_c) - (loss_fn(model, t_u, w, b-delta), t_c)) / (2.0*delta)

w -= learning_rate * loss_rate_of_change_w
b -= learning_rate * loss_rate_of_change_b

上面这种方法会存在误差，可以考虑采用链式法则进行导数的计算：

def loss_fn(t_p, t_c):
  squared_diffs = (t_p - t_c)**2
  return squared_diffs.mean()

def dloss_fn(t_p, t_c):
  dsq_diffs = 2 * (t_p - t_c)
  return dsq_diffs

def model(t_u, w, b):
  return w * t_u + b

def dmodel_dw(t_u, w, b):
  return t_u

def dmodel_db(t_u, w, b):
  return 1.0

def grad_fn(t_u, t_c, t_p, w, b):
  dloss_dw = dloss_fn(t_p, t_c) * dmodel_dw(t_u, w, b)
  dloss_db = dloss_fn(t_p, t_c) * dmodel_db(t_u, w, b)
  return torch.stack([dloss_dw.mean(), dloss_db.mean()])	# 利用stack合成一个tensor

对于一个训练轮次可以写成下面的样子：

def training_loop(n_epochs, learning_rate, params, t_u, t_c):
  for epoch in range(1, n_epochs+1):
    w, b = params
    
    t_p = model(t_u, w, b)
    loss = loss_fn(t_p, t_c)
    grad = grad_fn(t_u, t_c, t_p, w, b)
    
    params = parmas - learning_rate * grad
    
    print("Epoch %d, Loss %f" % (epoch, float(loss)))
  return params

对于不同的参数，可能得到的梯度大小会很不一样，一般将所有的输入做一个标准化的操作，从而能够使得训练更有效的收敛。

Autograd

autograd可以自动的根据运算求出导数，而不需要手动的对复杂的函数进行计算，考虑用autograd重写之前的内容：

def model(t_u, w, b):
  return w * t_u + b

def loss_fn(t_p, t_c):
  squared_diffs = (t_p - t_c)**2
  return squared_diffs.mean()

params = torch.tensor([1.0, 0.0], requires_grad = True)

requires_grad的效果是让pytorch在运算过程中对他的值进行追踪，每个参数都有.grad对象，正常情况下值为None。

1 2	loss = loss_fn(model(t_u, params), t_c) # 加相当于对参数进行解包，分别作为w,b传入 loss.backward()

通过backward()反传之后，params.grad不再是None。

多次运算，params上的梯度会被叠加，为了防止这样的事情出现，需要将梯度清零：

1 2	if params.grad is not None: params.grad.zero_()

现在训练过程长这个样子：

def training_loop(n_epochs, learning_rate, params, t_u, t_c):
  for epoch in range(1, n_epochs + 1):
    if params.grad is not None:
      params.grad.zero_()
    
    t_p = model(t_u, *params)
    loss = loss_fn(t_p, t_c)
    loss.backward()
    
    params = (params - learning_rate * params.grad).detach().requires_grad_()
    
    if epoch % 500 == 0:
      print('Epoch %d, Loss %f' % (epoch, float(loss)))
  return params

detach将旧版本的参数从运算图中分离，requires_grad_使得参数可以被追踪导数。调用方法如下：

training_loop(
	n_epochs = 5000,
	learning_rate = 1e-2,
	params = torch.tensor([1.0,0.0], requires_grad = True),
	t_u = t_un,
	t_c = t_c)

Optimizer

可以通过下面的方法列出所有的优化器：

1
2
3

import torch.optim as optim

dir(optim)

每个优化器在构造的时候都针对一系列的参数(requires_grad = True)，每个参数都被存在优化器内部，使得可以通过访问grad来对他们进行更新。

每个优化器都有两个方法：zero_grad和step，前者将所有在构建优化器时候传入的参数的grad全部设置成0，后者通过优化器自己的方法利用梯度对参数进行更新。

params = torch.tensor([1.0, 0.0], requires_grad = True)
learning_rate = 1e-5
optimizer = optim.SGD([params], lr = learning_rate)

t_p = model(t_un, * params)
loss = loss_fn(t_p, t_c)
# 正常的流程
optimizer.zero_grad()
loss.backward()
optimizer.step()

更改之后的训练流程：

def training_loop(n_epochs, optimizer, params, t_u, t_c):
  for epoch in range(1, nepochs + 1):
    t_p = model(t_u, *params)
    loss = loss_fn(t_p, t_c)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if epoch%500 == 0:
      print('Epoch %d, Loss %f' % (epoch, float(loss)))
      
  return params

训练集，验证集和过拟合

规则一：如果训练loss不下降，那么可能是模型太简单，或者是输入的信息不能很好地解释输出

规则二：如果验证集loss偏离，说明过拟合

缓解过拟合方法：

添加正则项
给输入加噪声生成新的数据
采用更简单的模型

可以考虑利用随机排序的下标来获得shuffle后的训练集和验证集：

n_samples = t_u.shape[0]
n_val = int(0.2*n_sample)

shuffled_indices = torch.randperm(n_samples)

train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]

由于并不会考虑在验证集的loss上反向传播，为验证集构造运算图是非常浪费内存和时间的事情，可以考虑利用torch.no_grad来提升效率：

def training_loop(n_epochs, optimizer, params, train_t_u, val_t_u, train_t_c, val_t_c):
  for epoch in range(1, n_epochs + 1):
    train_t_p = model(train_t_u, *params)
    train_loss = loss_fn(train_t_p, train_t_c)
    
    with torch.no_grad():
      val_t_p = model(val_t_u, *params)
      val_loss = loss_fn(val_t_p, val_t_c)
      assert val_loss.requires_grad == False  # 确认所有参数的requires_grad是False
      
    optimizer.zero_grad()
    train_loss.backward()
    optimizer.step()

或者可以使用set_grad_enabled来条件的启用反向传播

def calc_forward(t_u, t_c, is_train):
  with torch.set_grad_enabled(is_train):
    t_p = model(t_u, *params)
    loss = loss_fn(t_p, t_c)
  return loss

[读书笔记] Deep Learning with Pytorch -- Chapter 3

发表于 2019-12-12

主要内容

如何用tensor对数据进行表示
如何将原始数据（raw data）处理成可用于深度学习的形式

Tabular Data

用CSV或者其他表格形式组织的表格数据是最易于处理的，不同于时间序列数据，其中的每个数据项都是独立的，不存在时序上的关系。面对多种数值型的和定类型的数据，我们需要做的是把他们全部转化为浮点数表示的形式。

winequality-whit.csv是一个用;进行分隔的csv文件，第一行为各种相关的数值。

利用numpy导入的方法如下：

wine_path = "./winequality-white.csv"
wine_numpy = np.loadtxt(wine_path, dtype = np.float32, delimiter = ';', skiprows = 1)

wineq = torch.from_numpy(wine_numpy)

其中delimiter每行中分隔元素的分隔符。

将score从输入中分离：

1
2
3

data = wineq[:, :-1]

target = wineq[:, -1]

将score作为一个定类型的数据，用one_hot向量来表示

# 将target作为一个整数组成的向量
target = target.long()

target_onehot = torch.zeros(target.shape[0], 10)
target_onehot.scatter_(1, target.unsqueeze(1), 1.0)

由于下划线，scatter_是原地修改的，其中三个参数的意义如下：

指示后面两个参数操作对应的维度
一列tensor用来指示分散元素的下标
一个包含有分散元素的tensor，或者一个单一的向量或标量

unsqueeze把本来是4898大小的一维tensor转换成了size为4898x1大小的二维tensor。

可以对输入做一个标准化的处理：

data_mean = torch.mean(data, dim=0)
data_var = torch.var(data, dim=0)

data_normalized = (data - data_mean) / torch.sqrt(data_var)

同时可以考虑使用le，lt，gt，ge方法简单的进行划分

# le的返回值是一个0,1的tensor，可以直接用于索引
bad_indexes = torch.le(target, 3)
bad_data = data[bad_indexes]

bad_data = data[torch.le(target, 3)]
min_data = data[torch.gt(target, 3) & torch.lt(target, 7)]
good_data = data[torch.ge(target, 7)]

Time series

采用的数据集为https://archive.ics.uci.edu/ml/datasets/bike+sharing+dataset

bikes_numpy = np.loadtxt("hour-fixed.csv",
                        dtype = np.float32,
                        delimiter = ',',
                        skiprows = 1,
                        converters = {1: lambda x: float(x[8:10])})
# converters 用于把日期的字符串中的天数给提取出来并转换成数字
bikes = torch.from_numpy(bikes_numpy)

在这种时间序列数据中，行是按照连续的时间点进行有序排列的，所以不能把每一行当做一个独立的数据项进行处理。

对每个小时有的数据如下：

instant 	# index of record
day 		# day of month
season 		# season (1: spring, 2: summer, 3: fall, 4: winter)
yr 		# year (0: 2011, 1: 2012)
mnth 		# month (1 to 12)
hr 		# hour (0 to 23)
holiday	 	# holiday status
weekday 	# day of the week
workingday 	# working day status
weathersit 	# weather situation
		# (1: clear, 2:mist, 3: light rain/snow, 4: heavy rain/snow)
temp 		# temperature in C
atemp 		# perceived temperature in C
hum 		# humidity
windspeed 	# windspeed
casual 		# number of causal users
registered 	# number of registered users
cnt		# count of rental bikes

神经网络需要看到一个序列的输入，是 $N$ 个大小为 $C$ 的平行序列， $C$ 代表channel，就如同一维数据中的column， $N$ 表示时间轴上的长度。

数据集的大小为(17520, 17)的，下面把它改为三个维度（天数，小时，信息）：

1	daily_bikes = bikes.view(-1, 24, bikes.shape[1])

使用view方法不会改变tensor的存储，事实上只是改变了索引的办法，是没有什么开销的。这样实际上就得到了N个24连续小时，有7个channel组成的块。如果要得到所希望的 $N\times C\times L$ 的数据，可以采用transpose：

1	daily_bikes = daily_bikes.transpose(1, 2)

天气情况实际上是一个定类型的数据，可以考虑把它改成onehot的形式

daily_weather_onehot = torch.zeors(daily_bikes.shape[0], 4 daily_bikes.shape[2])

daily_weather_onehot.scatter_(1,
                              daily_bikes[:,9,:].long().unsequeeze(1)-1,
                             1.0)
# -1是为了从1~4变为0~3
daily_bikes = torch.cat((daily_bikes, daily_weather_onehot), dim=1)

# 可以采用这种mask的方法删除掉原来的列
daily_bikes = daily_bikes[:, torch.arange(daily_bikes.shape[1])!=9, :]

Text

深度学习采用基于循环神经网络的方法，在许多的NLP任务上都达到了SOTA的水平，这一章主要讲怎么把文本数据进行组织。采用的数据是《Pride and Prejudice》。

1 2	with open('1342-0.txt', encoding = 'utf-8') as f: text = f.read()

onehot

一种最为简单的方法就是onehot方法，在这里先考虑字母级别的，可以考虑将所有字母都转换成小写，从而减少需要encoding的量，或者可以删掉标点，数字等于任务没有什么关系的内容。

# line是text里面的任意一行
letter_tensor = torch.zeros(len(line), 128)

for i, letter in enumerate(line.lower().strip()):
  letter_index = ord(letter) if ord(letter) < 128 else 0
  letter_tensor[i][letter_index] = 1

对于词语级别的，可以通过构建一个词语表来完成：

def clean_words(input_str):
  punctuation = '.,;:"!?”“_-'
  word_list = input_str.lower().replace('\n',' ').split()
  word_list = [word.strip(punctuation) for word in word_list]
  return word_list

words_in_line = clean_words(line)

# 构造一个从词语到索引的映射
word_list = sorted(set(clean_words(text)))
word2index_dict = {word: i for (i, word) in enumerate(word_list)}

# 完成tensor的构建
word_tensor = torch.zeros(len(words_in_line), len(word2index_dict))
for i, word in enumerate(words_in_line):
  word_index = word2index_dict[word]
  word_tensor[i][word_index] = 1

embedding

Onehot是一种简单方法，但是存在很多缺点：

当语料库很大的时候，单词表会变得异常庞大
每次出现一个新单词，都要修改单词表，改变tensor的维度

embedding是一种把单词映射到高维的浮点数向量的方法，以便用于下游的深度学习任务。想法就是，相近的词语，在高维的空间中有更接近的距离。

Word2vec是一个确切的算法，我们可以通过一个利用上下文预测词语的任务，利用神经网络从onehot向量训练出embedding。

Images

通过排列在规律网格中的标量，可以表示黑白图片，如果每个格点利用多个标量来表示的话，可以描述彩色图片，或者例如深度之类的其他feature。

可以利用imageio来加载图片

improt imageio

img_arr = imageio.imread('bobby.jpg')
img_arr.shape
# Out: (720, 1280, 3)

在PyTorch里面，对于图片数据采用的布局是 $C\times H\times W$ 的（通道，高度，宽度）。可以使用transpose进行转换。

1 2	img = torch.from_numpy(img_arr) out = torch.transpose(img, 0, 2)

对于大量的图片导入，预先分配空间是一个更为有效的方法：

batch_size = 100
batch = torch.zeros(100, 3, 256, 256, dtype=torch.uint8)

import os

data_dir = "image-cats/"
filenames = [name for name in os.listdir(data_dir) if os.path.splitext(name) == '.png']
for i, filename in enumerate(filenames):
  img_arr = imageio.imread(filename)
  batch[i] = torch.transpose(torch.from_numpy(img_arr), 0, 2)

由于神经网络对0~1范围内的数值能够鞥有效的处理，所以一般会采用下面的处理方法：

# 直接处理
batch = batch.float()
batch /= 255.0

# 对每个channel标准化
n_channels = batch.shape[1]
for c in range(n_channels):
  mean = torch.mean(batch[:, c])
  std = torch.std(batch[:, c])
  batch[:, c] = (batch[:, c] - mean) / std

同时可以考虑对图片进行旋转，缩放，裁剪等操作，进行数据增强，或者通过修改来适应神经网络的输入尺寸。

Volumetric data

除去一般的2D图像，还可能处理类似CT图像这样的数据，是一系列堆叠起来的图片，每一张代表一个切面的信息。本质上来说，处理这种体积的数据和图片数据没有很大区叠，只不过会增加一个深度维度，带来的是一个 $N\times C\times H \times W \times D$ 的五维tensor。

同样可以采用imageio库进行加载：

import imageio

dir_path = 'volumetric-dicom/2-LUNG 3.0 B70f-04083'
vol_arr = imageio.volread(dir_path, 'DICOM')
vol_arr.shape

# OUT: (99, 512, 512)

vol = torch.from_numpy(vol_arr).float()
vol = torch.transpose(vol, 0, 2)
vol = torch.unsqueeze(vol, 0)
vol.shape

# OUT: (1, 512, 512, 99)

[读书笔记] Deep Learning with Pytorch -- Chapter 2

发表于 2019-12-10

啥是深度学习

Input Representation -> Intermediate Representation -> Output Representation

神经网络学到的就是怎样把Input Representation转化成Output Representation。

Tensor

PyTorch中的tensor起始就是一个n维数组，可以和NumPy中的ndarray相类比，Tensor支持numpy的无缝衔接。

对比NumPy中的ndarray，tensor可以

在GPU上进行高效的运算
可以在多机器上进行运算
可以在运算图上进行追踪

Tensor基础

Python内置List的不足点

浮点数会使用超过32bit的大小来进行储存，数据量打的时候比较低效
不能从向量化的运算中得到优化，在内存中并不都是连续分布的
对于多维的情况只能写list的list，十分的低效
python解释器和优化编译过后的代码相比比较低效，用C做底层会快很多

可以类似numpy中的索引方式。

可以利用torch.zeros(3,2)或者torch.ones(3,2)的函数进行初始化。

Tensor存储

存储形式类似C中数组的方式。

可以利用tensor.storage()方法获得连续的存储，无论本来是几维数组，都可以最终得到一个连续的数组，用正常方法进行索引。类似于得到C中多维数组的首地址。

通过改变storage中的值同样可以改变对应tensor的内容。

Size, storage offset, and strides

Size：一个tuple，能告诉这个tensor的每一维有多少元素，tensor.size()或者tensor.shape
Storage offset：相对于tensor中第一个元素的offset，tensor.storage_offset()
Stride：每一维度上，所需要得到下一个元素的步长，tensor.stride()

注意：子tensor有着更少的维度，但是实际上有着和原来的tensor都在相同的地方存储，所以对子tensor的改变会改变原来的tensor（直接类比C语言中的多维数组）。可以采用tensor.clone()得到tensor的克隆，这样更改不会改变原来的tensor。

tensor.t()可以将tensor转置，但是他们的存储空间仍然是一样的，只是改变了size和stride。确切的说，只是把对应维度的size和stride进行了交换。

tensor.transpose()可以用来对多维数组的两个维度进行交换，接受两个参数，分别代表dim0和dim1。

contiguous表示tensor在存储中是否按照直接的形式进行存储。可以用tensor.is_contiguous()进行判断，并且可以用tensor.contiguous方法对存储重新排布，不改变size，改变storage和stride。

数值类型

在创建的时候可以用dtype进行指定，默认的是32-bit浮点数，torch.Tensor就是torch.FloatTensor的别名，下面是一些可能的值：

torch.float32 or torch.float—32-bit floating-point
torch.float64 or torch.double—64-bit, double-precision floating-point
torch.float16 or torch.half—16-bit, half-precision floating-point
torch.int8—Signed 8-bit integers
torch.uint8—Unsigned 8-bit integers
torch.int16 or torch.short—Signed 16-bit integers
torch.int32 or torch.int—Signed 32-bit integers
torch.int64 or torch.long—Signed 64-bit integers

可以通过tensor.dtype来获取类型，可以用对应的方法或者to()进行转换，type()进行同样的操作，但是to()还可以接受额外的参数。

double_points = torch.zeros(10,2).double()
short_points = torch.ones(10,2).short()

double_points = torch.zeros(10,2).to(torch.double)
short_points - torch.ones(10,2).to(dtype = torch.short)

points = torch.randn(10,2)
stort_points = points.type(torch.short)

tensor索引

正常的列表索引，不同维度上切片什么的随你玩

与NumPy的交互

利用tensor.numpy()把tensor转换为numpy中的array。利用tensor.from_numpy()把numpy中的array转换成tensor。

注意一点，如果tensor在CPU上分配的话，是共享存储的，但是如果在GPU上分配的话，会在CPU上重新创造一个array的副本。

Serializing Tensor

tensor的保存与加载，即可以使用路径，也可以使用文件描述符

# Save
torch.save(points, '../data/p1ch3/ourpoints.t')

with open('../data/p1ch3/ourpoints.t','wb') as f:
    torch.save(points, f)

# Load
points = torch.load('../data/p1ch3/ourpoints.t')

with open('../data/p1ch3/ourpoints.t','rb') as f:
    torch.load(f)

如果要将tensor保存成一个更加可互用的形式，可以采用HDF5格式，一种用于表示多维数组的格式，他内部采用一个字典形式的键值对来进行保存。python通过h5py库支持HDF5格式，它可以接受和返回NumPy array。

import h5py

f = h5py.File('../data/plch3/ourpoints.hdf5','w')
dset = f.create_dataset('coords', data = points.numpy())
f.close()

在这里’coords’就是key，有趣的一点在于可以只从HDF5中加载一部分的内容，而不用加载全部！

1
2
3

f = h5py.File('../data/p1ch3/ourpoints','r')
dset = f['coords']
last_points = dset[1:]

在这种情况下只取出了后面几个点的坐标，返回了一个类似NumPy数组的对象。可以直接采用from_numpy()方法构造tensor。

这种情况下，数据会复制到tensor的storage。

1 2	last_points = torch.from_numpy(dset[1:]) f.close()

记得在加载完数据之后关闭文件！

将tensor移动到GPU

在GPU上可以对tensor进行高效的并行计算，tensor有一个device可以用来指定在CPU或者GPU上面，可以在创建时候指定，或者利用to方法创建一个GPU上的副本。

points_gpu = torch.tensor([[1.0, 4.0], [2.0, 1.0], [3.0, 4.0]],
                          device='cuda')

points_gpu = points.to(device='cuda')

注意！这个时候类型会从torch.FloatTensor变成torch.cuda.FloatTensor，其他的类型类似。

如果有多GPU的情况，可以用一个从零开始的int来指定特定的GPU，如下

1	points_gpu = points.to(device='cuda:0')

注意到一个问题，运算结束后，并不会把结果返回到CPU，只是返回一个handle，除非调用了to方法把它弄回了CPU。

可以使用cuda()方法和cpu()方法完成类似上面的事情

1
2
3

points_gpu = points.cuda() #默认是分配到下标为0的GPU
points_gpu = points.cuda(0)
points = points_gpu.cpu()

但是使用to方法可以传递多个参数！比如同时改变device和dtype。

Tensor API

注意有些api会在最后有一个下划线，表示他们是原地修改的，并不会返回一个新的tensor，例如zero_()会原地把矩阵清零。如果没有下划线会返回一个新的tensor，而原tensor保持不变。大致的API分类如下：

Creation ops—Functions for constructing a tensor, such as ones and from_numpy
Indexing, slicing, joining, and mutating ops—Functions for changing the shape,

stride, or content of a tensor, such as transpose

Math ops—Functions for manipulating the content of the tensor through computations:
- Pointwise ops—Functions for obtaining a new tensor by applying a function to each element independently, such as abs and cos
- Reduction ops—Functions for computing aggregate values by iterating through tensors, such as mean, std, and norm
- Comparison ops—Functions for evaluating numerical predicates over tensors, such as equal and max
- Spectral ops—Functions for transforming in and operating in the frequency domain, such as stft and hamming_window
- Other ops—Special functions operating on vectors, such as cross, or matrices, such as trace
- BLAS and LAPACK ops—Functions that follow the BLAS (Basic Linear Algebra Subprograms) specification for scalar, vector-vector, matrix-vector, and matrix-matrix operations
Random sampling ops—Functions for generating values by drawing randomly

from probability distributions, such as randn and normal
Serialization ops—Functions for saving and loading tensors, such as load and

save

Parallelism ops—Functions for controlling the number of threads for parallel

CPU execution, such as set_num_threads

[读书笔记] Deep Learning with Pytorch -- Chapter 1

发表于 2019-12-10

PyTorch拥有的工具

自动求导：torch.autograd
数据加载与处理：torch.util.data
- Dataset
- DataLoader
  生成子进程从Dataset加载数据
多GPU或者多机器训练：torch.nn.DataParallel, torch.distributed
优化器：torch.optim

Hello World!

发表于 2019-11-02

Hello ?

Hello !