0%

[论文笔记] A Survey of Model Compression and Acceleration

发表于

这是一篇模型压缩领域的综述，主要从参数剪枝和量化（Parameter pruning and quantization），低秩分解（Low-rank factorization），转移/紧致卷积滤波器（Transferred/compact convolutional filters）和知识蒸馏（Knowledge distillation）四个方面来对于已有的模型压缩方法进行综述。这篇文章发表的时间点为2017年，可能对于较新的成果涉及并不是那么广泛，但是对于模型压缩加速领域的一个初步了解而言感觉还是可以的。

四个方向的总体概览如下所示：

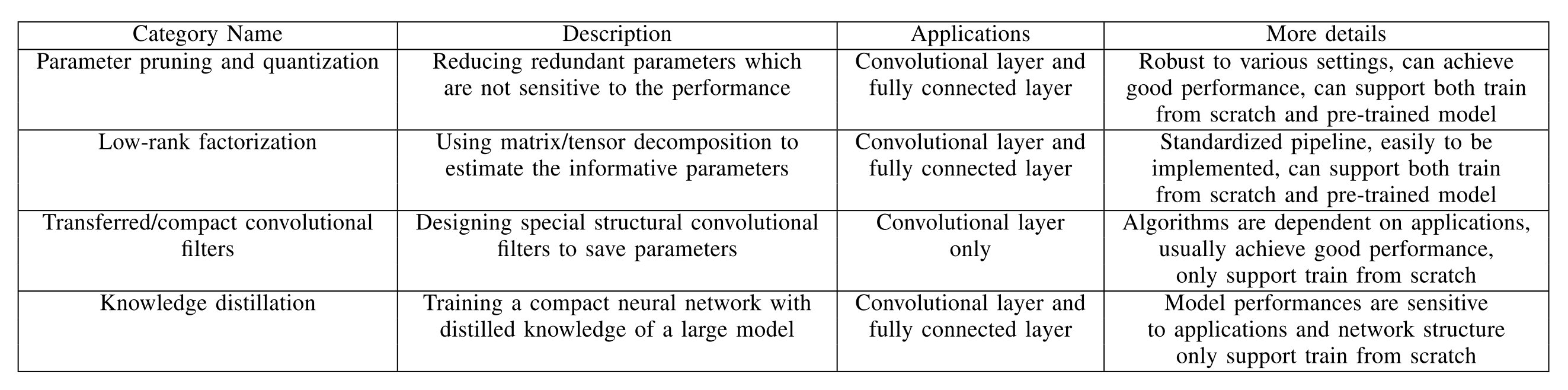
参数剪枝和量化（Parameter pruning and quantization）

量化与二值化（Quantization and Binarization）

网络量化是通过用来表示权重的bits数目来将原网络进行压缩的，比如可以采用16-bit浮点或者是8-bit整数来表示权重，极限情况下可以采用1-bit的二进制权重神经网络。

同时也有一种方法是通过权重共享来实现模型的压缩，可以认为是通过Hash方法将所有近似的权重对应于一个Hash值，即使得相同的权重只被存放一次。这里通过哈夫曼编码来减少存放索引所需要的空间，从而可以通过索引去读取对应的内容。

流程如下所示：

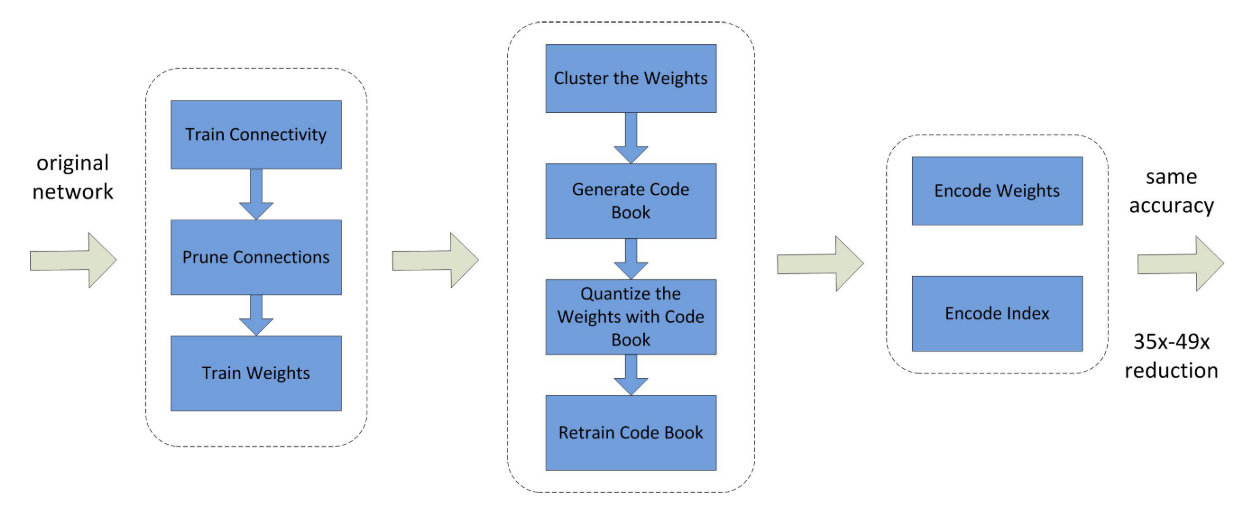
他实际上在利用Code Book量化之后会对共享的权重进行重训，来得到更好的效果。最后得到的就是权重的Code Book，每个权重存放的是对应的索引而不是权值。

（好奇.jpg，离散值的梯度反传等等怎么搞？找到了个知乎链接，有空看看，估摸着是不一定会看了)

缺点：

  • 二进制网络的精度降低非常严重。
  • 当前的二进制方案基于简单的矩阵估计，忽略了二进制在精度损失方面的效果。

网络剪枝（Network Purning）

网络剪枝和共享已经被用于减少网络复杂性和处理过拟合任务。一个早些的剪枝方法是有偏的权重衰减。最优脑损害(The Optimal Brain Damage)和最优脑外科医生(the Optimal Brain Surgeon)方法基于损失函数Hessian矩阵来减少连接层的参数，这些工作期望能够比基于大小的剪枝方法（比如权重衰减）有更高的准确率。

网络剪枝的最近一个方向是剪枝掉预训练模型当中的冗余权重，通过data-free的方式来去除掉冗余的神经元和连接。

同时也有一个方向是训练带有稀疏性约束的CNN网络。在最优化问题当中，稀疏性约束通常就是l0l_0和l1l_1正则化。

缺点：

  • 利用l1l_1或者是l2l_2正则化通常需要更多的迭代来收敛
  • 所有的剪枝条件都一定程度上需要人工来设置网络层的敏感性
  • 网络剪枝通常能够降低模型大小但是没有办法提升效率

构造结构化矩阵（Designing Structural Matrix）

结构化矩阵的方式从我的理解来看，实际上就是通过更少的参数来表示全连接层的那个大矩阵，从而降低需要的参数量。由于有的结构化方法可以通过特性进行高效的矩阵-向量乘法，所以不仅可以降低内存的消耗，同时可以加速模型的训练和推断。

（好奇.jpg x 2，卷积实际上应该也是一种结构化矩阵，这玩意能不能在受限情况下进行搜索？）

一种方法就是通过循环投影（circulant projections），通过向量r=(r0,r1,…,rd−1)\mathbf{r}=(r_0,r_1,\ldots,r_{d-1})，一个循环矩阵R∈Rd×d\mathbf{R}\in \mathbf{R}^{d\times d}可以如下定义：

R=circ(r):=[r0rd−1…r2r1r1r0rd−1r2⋮r1r0⋱⋮rd−2⋱⋱rd−1rd−1rd−2…r1r0]\mathbf{R}=\text{circ}(\mathbf{r}):=\left[\begin{array}{ccccc} r_{0} & r_{d-1} & \ldots & r_{2} & r_{1} \\ r_{1} & r_{0} & r_{d-1} & & r_{2} \\ \vdots & r_{1} & r_{0} & \ddots & \vdots \\ r_{d-2} & & \ddots & \ddots & r_{d-1} \\ r_{d-1} & r_{d-2} & \ldots & r_{1} & r_{0} \end{array}\right]

这使得内存消耗从O(d2)O(d^2)变成了O(d)O(d)，同时循环矩阵也可以利用快速傅立叶变换（FFT）来加速计算过程。提供一个dd维的向量，通过上述矩阵的计算时间复杂度为O(dlogd)O(d\log d)。

缺点：

  • 结构化约束会使得模型有偏，损害模型的性能（我的角度来看就是做了不该做的假设）

  • 很难找到合适的结构化矩阵，当前也缺乏理论指导

低秩分解（Low-rank factorization）

卷积操作占据了深度CNNs模型中的最大计算篇幅，因此减少卷积层能够提升压缩率同时也能加快运算速度。

对于卷积核，它可以被认为一个4D张量。基于张量分解的想法驱使我们本能的认为4D张量的冗余性去除会有一个显著提升，这是一个特殊的方式去移除冗余性。注意到全连接层，它能够被视为一个2D矩阵并且低秩也能有所帮助。

很长时间以来，人们使用低秩滤波器去加速卷积，例如，高维DCT（discrete cosine transform,）和小波系统（wavelet systems）各自使用张量积去构造从一维DCT和小波。

低秩估计是逐层而做的。一层的参数在低质估计后固定下来，而上面的层是微调基于一个重构误差准则。这些是典型的用于压缩2D卷积滤波器的低秩估计方法。根据这个方向，Canonical Polyadic(CP)分解是一个用于核张量的方法。人们使用非线性的最小二乘去计算CP分解。然而，找到最好的低秩估计在CP分解中式一个病态问题，并且最好的rank−Krank-K（K是秩的值）估计可能是不存在的。

正如前面所提，全连接层可以看成是2D矩阵，因此上述的方法（指低秩估计的方法）也能够应用到这儿（指全连接层的分解）。也有工作应用截断奇异值分解去分解全连接层用于设计紧凑的多任务深度学习框架。

缺点：

  • 低秩方法涉及到计算代价昂贵的分解操作，执行起来并不容易。
  • 由于不同层有着不同的信息，当前的低秩估计方法是逐层的，因此不能执行全局的参数压缩。
  • 比较原始模型， 分解需要额外的再训练去实现收敛。

转移/紧致卷积滤波器（Transferred/compact convolutional filters）

CNNs 是参数有效的对于转换的不变性，对于输入图片表示的不变性，而这对于训练深度模型而不导致过拟合是重要的。尽管目前还缺失强理论证明，但是大量的经验事实支持平移不变性和权重共享对于好的预测性能是重要的。 使用转移卷积滤波器去压缩CNN模型的想法受到研究工作启发，它引入了等价理论。让xx是一个输入，Φ(⋅)\Phi(\cdot)是一个网络层和T(⋅)\mathcal{T}(\cdot)是一个转换矩阵。等价性的概念如下所定义：

T′(Φ(x))=Φ(Tx)\mathcal{T}^\prime(\Phi(x)) = \Phi(\mathcal{T}x)

表明转换了T(⋅)\mathcal{T}(\cdot) 的输入 xx 然后传递它到层次Φ(⋅)\Phi(\cdot)的网络（即得到Tx\mathcal{T}x后再用网络作用）应该有同样的结果在第一次用网络映射xx然后再转换表示（即先得到Φ(x)\Phi(x)，再用T\mathcal{T}作用)。注意：T′(⋅)\mathcal{T}^\prime(\cdot)和T(⋅)\mathcal{T}(\cdot)不是必须相同的。根据这个理论，应用转换层或者滤波器Φ(⋅)\Phi(\cdot)去压缩整个网络模型是合理的。从经验观察，深度CNNs同样受益于使用大的卷积滤波器通过应用确定的转换T(⋅)\mathcal{T}(\cdot)到一个小的基础偏置滤波器的集合，由于它扮演了一个模型的正则化。

在这个方向，有许多最近的研究工作去建立一个由基础滤波集合构建的卷积层。（就是从不同的角度定义函数 T(⋅)\mathcal{T}(\cdot)）

缺点：

  • 这些方法能够对于宽度（扁平）的框架（比如VGGNet）能够实现竞争性的性能，但是对于深度的网络（比如GoogleNet，ResNet）效果就不是很好。
  • 指导学习的转移假设条件有时太强了，这使得结构对于某些情形是不稳定的。

知识蒸馏（Knowledge Distillation）

知识蒸馏的基本想法就是将深度大模型中蒸馏知识到一个浅层的网络当中。压缩的网络会尝试学习深层复杂网络的这样一个映射。通常的方法就是通过学习softmax之后的分布来讲大模型的知识蒸馏到小模型当中。当然也有一些工作来尝试学习高层隐层当中的表征，或者是feature maps来进行知识蒸馏，以获得相对于最终的分布更多的信息。通常而言大模型和压缩模型的容量结构相差比较大，假设其中间结果有着相似效果是一个过强的约束。

缺点：

  • 知识蒸馏的方法可以显著降低运算量，但是只能够被用在softmax loss的任务上。
  • 只能够从头开始训练，不能够从已有的模型权重当中进行抽取。
  • 效果相对于其他方法而言也并不够好。

评测指标与数据集

数据集

数据集主要为主流的图像相关任务数据集，对应的Baseline模型为主流的CV经典模型，如ResNet，VGG nets等。

评测指标

记MM为模型，aa为模型所含有的参数数量，ss为模型的运行时间，大部分工作是采用的平均每epoch的训练时间，但是实际上测试时间也是可以的。利用M∗M^*的星号上标来表示压缩后模型的对应指标，通常采用的评价指标有以下几种：

  • 压缩比率（compression rate）

    α(M,M∗)=aa∗\alpha(M, M^*) = \frac{a}{a^*}

  • 索引空间节省量（index space saving）

    β(M,M∗)=a−a∗a∗\beta(M, M^*) = \frac{a - a^*}{a^*}

  • 加速比率（speedup rate）

    δ(M,M∗)=ss∗\delta(M,M^*) = \frac{s}{s^*}

通常而言压缩比和加速比是高度相关的，因为越小的模型通常跑的越快。事实上在不同的任务当中这可能和不同的层类型是相关的。大多是任务的运算主要集中在全连接层，但是对图像分类任务而言，绝大多数的运算主要集中在卷积层，因为一开始的图像面积比较大，卷积层运算非常耗时间。所以具体的压缩和加速方法需要对应于不同的应用着重关注不同类型的网络层。