0%

Variational Inference

发表于

先回顾一下全贝叶斯推断：

训练阶段：

p(θ∣Xtr,Ytr)=p(Ytr∣Xtr,θ)p(θ)∫p(Ytr∣Xtr,θ)p(θ)dθp(\theta|X_{tr},Y_{tr}) =\frac{p(Y_{tr}|X_{tr},\theta)p(\theta)}{\color{red}{\int p(Y_{tr}|X_{tr},\theta)p(\theta) d\theta}}

测试阶段：

p(y∣x,Xtr,Ytr)=∫p(y∣x,θ)p(θ∣Xtr,Ytr)dθp(y|x,X_{tr},Y_{tr}) =\color{red}{\int p(y|x,\theta) p(\theta|X_{tr},Y_{tr})d\theta }

红色分布难以计算，使得后验分布只有在面对简单的共轭模型才能被精确求解

Approximate inference

概率模型：p(x,θ)=p(x∣θ)p(θ)p(x,\theta)=p(x|\theta)p(\theta)

变分推断（Variational Inference）：

采用一个简单的分布来近似后验：p(θ∣x)≈q(θ)∈Qp(\theta|x)\approx q(\theta)\in \mathcal{Q}

  • 有偏的
  • 高效并且可拓展

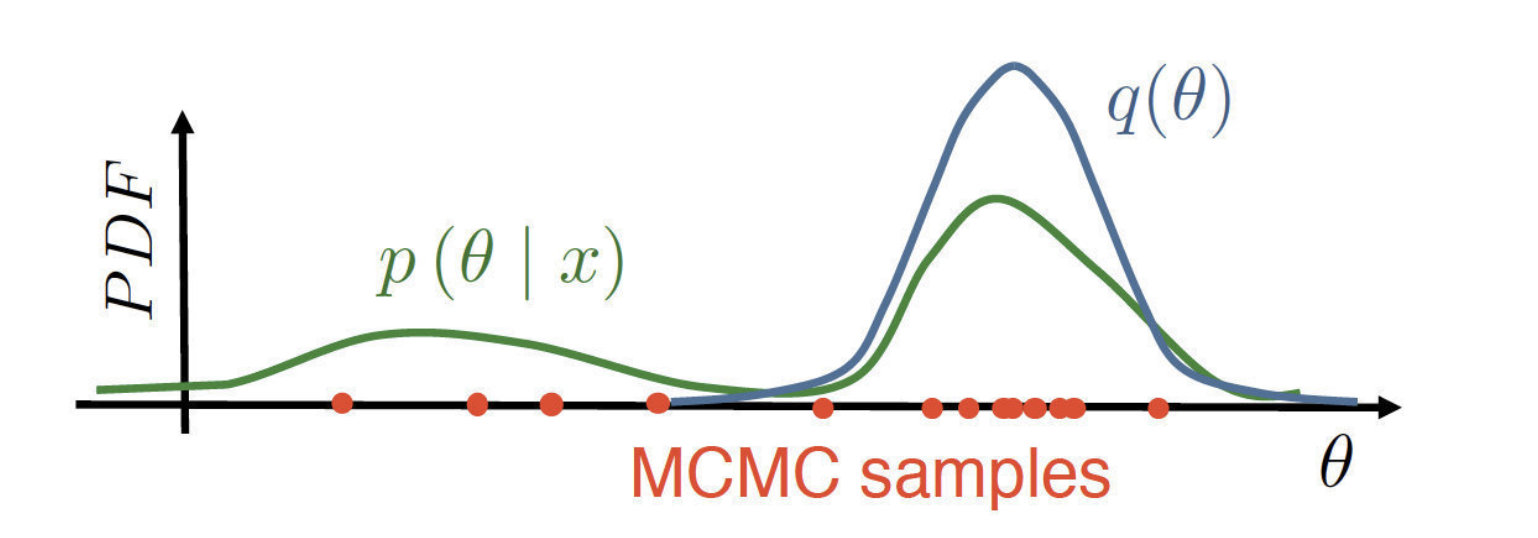
蒙特卡洛方法（MCMC）：

从没有标准化的p(θ∣x)p(\theta|x)里面进行采样（因为下面归一化的部分难以计算）：

  • 无偏的
  • 需要很多的采样才能近似

Variational inference

logp(x)=∫q(θ)logp(x)dθ=∫q(θ)logp(x,θ)p(θ∣x)dθ=∫q(θ)logp(x,θ)q(θ)p(θ∣x)q(θ)dθ=∫q(θ)logp(x,θ)q(θ)dθ+∫q(θ)logq(θ)p(θ∣x)dθ=L(q(θ))+KL(q(θ)∣∣p(θ∣x))\begin{aligned} \log p(x) &= \int q(\theta)\log p(x) d\theta =\int q(\theta)\log \frac{p(x,\theta)}{p(\theta|x)}d\theta\\ &=\int q(\theta)\log \frac{p(x,\theta)q(\theta)}{p(\theta|x)q(\theta)}d\theta\\ &=\int q(\theta)\log \frac{p(x,\theta)}{q(\theta)}d\theta + \int q(\theta)\log\frac{q(\theta)}{p(\theta|x)}d\theta\\ &=\color{green}{\mathcal{L}(q(\theta))}+ \color{red}{KL(q(\theta)||p(\theta|x))} \end{aligned}

前面的绿色部分是ELBO(Evidence lower bound)

后面的红色部分是用于变分推断的KL散度，KL散度越小，说明我们的估计与后验分布越接近

但是后验分布是未知的，否则就不需要求解了，再看一遍上面这个公式：

logp(x)=L(q(θ))+KL(q(θ)∣∣p(θ∣x))\log p(x) = \mathcal{L}(q(\theta)) + KL(q(\theta)||p(\theta|x))

可以发现前面logp(x)\log p(x)与q(θ)q(\theta)是没有关系的，那么要最小化KL散度，实际上就相当于最大化ELBO：

KL(q(θ)∣∣p(θ∣x))→minq(θ)∈Q⇔L(q(θ))→maxq(θ)∈QKL(q(\theta)||p(\theta|x))\rightarrow\min_{q(\theta)\in \mathcal{Q}} \quad \Leftrightarrow \quad \mathcal{L}(q(\theta))\rightarrow\max_{q(\theta)\in\mathcal{Q}}

改写一遍变分下界：

L(q(θ))=∫q(θ)logp(x,θ)q(θ)dθ=∫q(θ)logp(x∣θ)p(θ)q(θ)dθ=Eq(θ)logp(x∣θ)−KL(q(θ)∣∣p(θ))\begin{aligned}\mathcal{L}(q(\theta))&=\int q(\theta)\log\frac{p(x,\theta)}{q(\theta)}d\theta\\ &=\int q(\theta)\log\frac{p(x|\theta)p(\theta)}{q(\theta)}d\theta\\ &= \color{green}{\mathbb{E}_{q(\theta)}\log p(x|\theta) } - \color{red}{KL(q(\theta)||p(\theta))} \end{aligned}

前面绿色的为数据项，后面红色的为正则项

最终的优化问题就在于：

L(q(θ))=∫q(θ)logp(x,θ)q(θ)dθ→maxq(θ)∈Q\mathcal{L}(q(\theta)) = \int q(\theta) \log \frac{p(x,\theta)}{q(\theta)}d\theta \quad \rightarrow \quad \max_{q(\theta)\in \mathcal{Q}}

问题的关键是，怎么对于一个概率分布进行最优化

Mean Field Variational Inference

Mean Field Approximation

L(q(θ))=∫q(θ)logp(x,θ)q(θ)dθ→maxq(θ)=q1(θ1)⋅…⋅qm(θm)\mathcal{L}(q(\theta)) = \int q(\theta)\log \frac{p(x,\theta)}{q(\theta)}d\theta \quad \rightarrow \quad \max_{q(\theta)=q_1(\theta_1)\cdot \ldots \cdot q_m(\theta_m)}

块坐标上升法（Block coordinate assent）:

每次都固定除了一个维度分布其他的部分{qi(θi)}i≠j\{q_i(\theta_i)\}_{i\ne j}，然后对一个维度上的分布进行优化

L(q(θ))→maxqj(θj)\mathcal{L}(q(\theta)) \quad \rightarrow \quad \max_{q_j(\theta_j)}

由于除了qj(θj)q_j(\theta_j)其他维度都是固定的，可以得到如下的数学推导：

L(q(θ))=∫q(θ)logp(x,θ)q(θ)=Eq(θ)logp(x,θ)−Eq(θ)logq(θ)=Eq(θ)logp(x,θ)−∑k=1mEqk(θk)logqk(θk)=Eqj(θj)[Eqi≠jlogp(x,θ)]−Eqj(θj)logqj(θj)+Const{rj(θj)=1Zjexp(Eqi≠jlogp(x,θ))}=Eqj(θj)logrj(θj)qj(θj)+Const=−KL(qj(θj)∣∣rj(θj))+Const\begin{aligned} \mathcal{L}(q(\theta)) &=\int q(\theta)\log \frac{p(x,\theta)}{q(\theta)}\\ &=\mathbb{E}_{q(\theta)}\log p(x,\theta) - \mathbb{E}_{q(\theta)}\log q(\theta)\\ &=\mathbb{E}_{q(\theta)}\log p(x,\theta) - \sum_{k=1}^m \mathbb{E}_{q_k(\theta_k)}\log q_k(\theta_k)\\ &=\mathbb{E}_{q_j(\theta_j)}\left[\mathbb{E}_{q_{i\ne j}}\log p(x,\theta)\right] - \mathbb{E}_{q_j(\theta_j)}\log q_j(\theta_j)+Const\\ &\left\{r_j(\theta_j) = \frac{1}{Z_j} \exp\left(\mathbb{E}_{q_{i\ne j}}\log p(x,\theta)\right)\right\}\\ &=\mathbb{E}_{q_j(\theta_j)} \log \frac{r_j(\theta_j)}{q_j(\theta_j)}+Const\\ &=-KL\left(q_j(\theta_j)||r_j(\theta_j)\right)+Const \end{aligned}

在块坐标下降中的每一步优化问题转化为了：

L(q(θ))=−KL(qj(θj)∣∣rj(θj))+Const→maxqj(θj)\mathcal{L}(q(\theta)) = -KL(q_j(\theta_j)||r_j(\theta_j)) + Const \quad \rightarrow \quad \max_{q_j(\theta_j)}

实际上就是要最小化KL散度，容易发现解为：

qj(θj)=rj(θj)=1Zjexp(Eqi≠jlogp(x,θ))q_j(\theta_j) = r_j(\theta_j) =\frac{1}{Z_j} \exp\left(\mathbb{E}_{q_{i\ne j}}\log p(x,\theta)\right)

Parametric variational inference

考虑对于变分分布的参数族：

q(θ)=q(θ∣λ)q(\theta) = q(\theta|\lambda)

限制在于，我们选择了一族固定的分布形式：

  • 如果选择的形式过于简单，我们可能不能有效地建模数据
  • 如果选择的形式足够复杂，我们不能保证把它训得很好来拟合数据

但这样就把变分推断就转变成了一个参数优化问题：

L(q(θ∣λ))=∫q(θ∣λ)logp(x,θ)q(θ∣λ)dθ→maxλ\mathcal{L}(q(\theta|\lambda)) = \int q(\theta|\lambda) \log\frac{p(x,\theta)}{q(\theta|\lambda)}d\theta \quad \rightarrow \quad \max_{\lambda}

只要我们能够计算变分下界(ELBO)对于θ\theta的导数，那么就可以使用数值优化方法来对这个优化问题进行求解

Summary

Full Bayesian inference p(θ∣x)p(\theta\mid x)
MP inference p(θ∣x)≈δ(θ−θMP)p(\theta\mid x)\approx\delta(\theta-\theta_{MP})
Mean field variational inference p(θ∣x)≈q(θ)=∏j=1mqj(θj)p(\theta\mid x)\approx q(\theta)=\prod_{j=1}^m q_j(\theta_j)
Parametric variational inference p(θ∣x)≈q(θ)=q(θ∣λ)p(\theta\mid x)\approx q(\theta)=q(\theta\mid\lambda)