0%

[论文笔记] Multivariate Time Series Imputation with Generative Adversarial Networks

发表于

基本介绍

传统处理数据集中缺失值一般有两种方法：

  1. 直接针对缺失值进行建模
    • 对于每个数据集，需要单独建模
  2. 对于缺失值进行填充得到完整数据集，再用常规方法进行分析
    • 删除法，会丢失到一些重要信息，缺失率越高，情况越严重
    • 用均值/中位数/众数填充，没有利用现有的其他信息
    • 基于机器学习的填充方法
      • EM
      • KNN
      • Matrix Factorization

考虑一个这样的数据，时间序列XX是T=(t0,…,tn−1)T=(t_0, \ldots, t_{n-1})的一个观测，X=(xt0,…,xti,…,xtn−1)⊤∈Rn×dX=\left(x_{t_{0}}, \ldots, x_{t_{i}}, \ldots, x_{t_{n-1}}\right)^{\top} \in \mathbb{R}^{n \times d}，例如：

X=[16 none 97 none 7 none 9 none  none 79],T=[0513]X=\left[\begin{array}{cccc}{1} & {6} & {\text { none }} & {9} \\ {7} & {\text { none }} & {7} & {\text { none }} \\ {9} & {\text { none }} & {\text { none }} & {79}\end{array}\right], T=\left[\begin{array}{c}{0} \\ {5} \\ {13}\end{array}\right]

利用mask矩阵M∈Rn×dM\in \mathbb{R}^{n \times d}来表示XX中的值存在与否，如果存在，Mtij=1M^{j}_{t_i}=1否则的话Mtij=0M^{j}_{t_i}=0。

总体的基本框架如下，generator从随机的输入中生成时间序列数据，discriminator尝试判别是真的数据还是生成的假数据，通过bp进行优化：

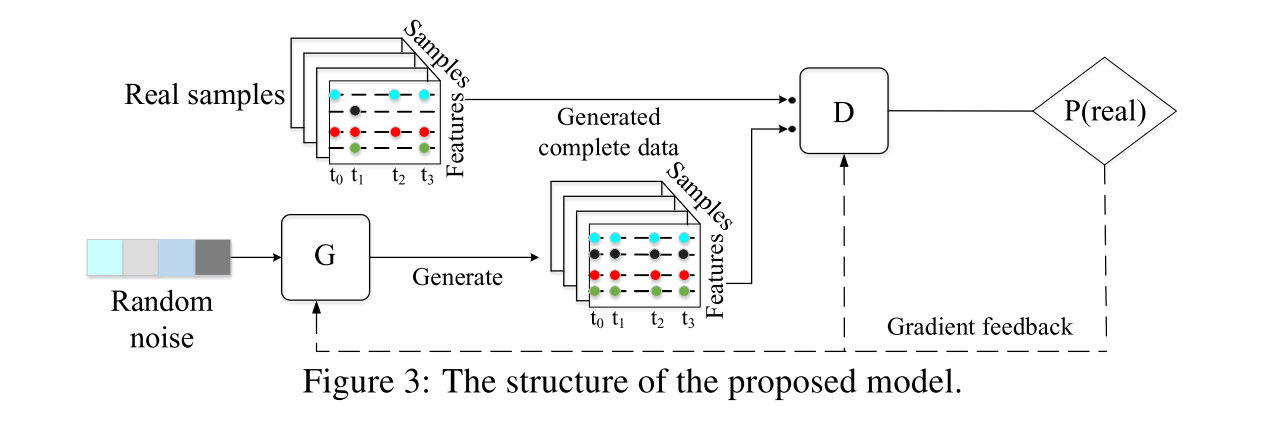
GAN框架

由于最初始的GAN容易导致模型坍塌的问题，采用WGAN（利用Wasserstein距离），他的loss如下：

LG=Ez∼Pg[−D(G(z))]LD=Ez∼Pg[D(G(z))]−Ex∼Pr[D(x)]\begin{array}{c}{L_{G}=\mathbb{E}_{z \sim P_{g}}[-D(G(z))]} \\ {L_{D}=\mathbb{E}_{z \sim P_{g}}[D(G(z))]-\mathbb{E}_{x \sim P_{r}}[D(x)]}\end{array}

采用基于GRU的GRUI单元作为G和D的基本网络，来缓解时间间隔不同所带来的的问题。可以知道的是，老的观测值所带来的影响随着时间的推移应当更弱，因为他的观测值已经有了一段时间的缺失。

时间衰减（time decay)

采用一个time lag矩阵δ∈Rn×d\delta\in \mathbb{R}^{n\times d}来表示当前值和上一个有效值之间的时间间隔。

δtij={ti−ti−1,Mti−1j==1δti−1j+ti−ti−1,Mti−1j==0&i>00,i==0;δ=[00005555813813]\delta_{t_{i}}^{j}=\left\{\begin{array}{ll}{t_{i}-t_{i-1},} & {M_{t_{i-1}}^{j}==1} \\ {\delta_{t_{i-1}}^{j}+t_{i}-t_{i-1},} & {M_{t_{i-1}}^{j}==0 \& i>0} \\ {0,} & {i==0}\end{array} \quad ; \quad \delta=\left[\begin{array}{cccc}{0} & {0} & {0} & {0} \\ {5} & {5} & {5} & {5} \\ {8} & {13} & {8} & {13}\end{array}\right]\right.

利用一个时间衰减向量β\beta来控制过去观测值的影响，每一个值都应当是在(0,1](0,1]的，并且可以知道的是，δ\delta中的值越大，β\beta中对应的值应当越小，其中WβW_{\beta}更希望是一个完全的矩阵而不是对角阵。

βti=1/emax(0,Wβδti+bβ)\beta_{t_i} = 1/ e^{\max(0,W_{\beta}\delta_{t_i}+b_{\beta})}

GRUI

GRUI的更新过程如下：

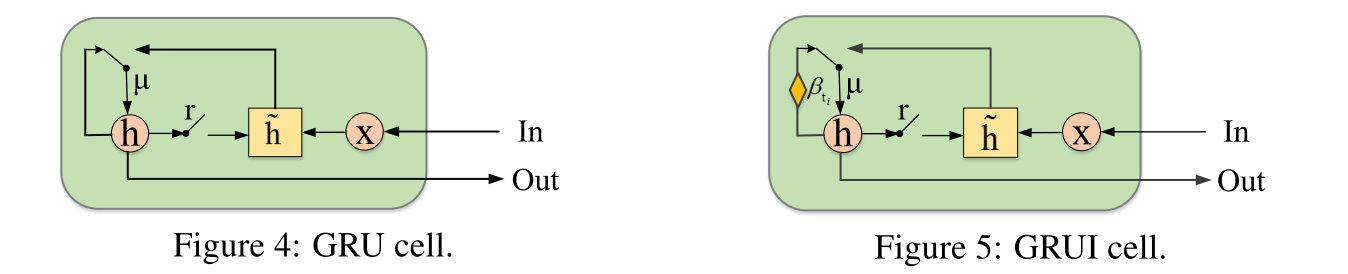
hti−1′=βti⊙hti−1μti=σ(Wμ[hti−1′,xti]+bμ)rti=σ(Wr[hti−1′,xti]+br)h~ti=tanh(Wh~[rti⊙hti−1′,xti]+bh~)hti=(1−μti)⊙hti−1′+μti⊙h~ti\begin{aligned}h_{t_{i-1}}^{\prime}&=\beta_{t_{i}} \odot h_{t_{i-1}}\\ \mu_{t_{i}} &= \sigma(W_{\mu}\left[h_{t_{i-1}}^{\prime},x_{t_{i}}\right]+b_{\mu}) \\ r_{t_{i}} &= \sigma(W_{r}\left[h_{t_{i-1}}^{\prime},x_{t_{i}}\right]+b_{r}) \\ \tilde{h}_{t_{i}} &= \tanh(W_{\tilde{h}}\left[r_{t_{i}} \odot h_{t_{i-1}}^{\prime},x_{t_{i}}\right]+b_{\tilde{h}})\\ h_{t_{i}}&=(1-\mu_{t_{i}})\odot h_{t_{i-1}}^{\prime}+\mu_{t_{i}}\odot \tilde{h}_{t_{i}}\end{aligned}

D和G的结构：

D过一个GRUI层，最后一个单元的隐层表示过一个FC（带dropout）

G用一个GRUI层和一个FC，G是自给的网络（self-feed network），当前的输出会作为下一个迭代的输入。最开始的输入是一个随机噪声。假数据的δ\delta的每一行都是常量。

G和D都采用batch normalization。

缺失值填补方法

考虑到xx的缺失，可能G(z)G(z)在xx没有缺失的几个值上面都表现的非常好，但是却可能和实际的xx差得很多。

文章中定义了一个两部分组成的loss function来衡量填补的好坏。第一部分叫做masked reconstruction loss，用来衡量和原始不完整的时间序列数据之间的距离远近。第二部分是discriminative loss，让生成的G(z)G(z)尽可能真实。

Masked Reconstruction Loss

只考虑没有缺失值之间的平方误差

Lr(z)=∥X⊙M−G(z)⊙M∥2L_{r}(z)=\|X \odot M-G(z) \odot M\|_{2}

Discriminative Loss

Ld(z)=−D(G(z))L_d(z) = -D(G(z))

Imputation Loss

Limputation(z)=Lr(z)+λLd(z)L_{imputation}(z) = L_{r}(z)+\lambda L_{d}(z)

对于每个原始的时间序列xx，从高斯分布中采样zz，通过一个已经训练好的GG获得G(z)G(z)。之后通过最小化Limputation(z)L_{imputation}(z)来进行训练，收敛之后用G(z)G(z)填充缺失的部分。

ximputed=M⊙x+(1−M)⊙G(z)x_{imputed} = M\odot x+(1-M)\odot G(z)