Codeforces 1363E - Tree Shuffling

原文

Ashish has a tree consisting of $n$ nodes numbered $1$ to $n$ rooted at node $1$. The $i$-th node in the tree has a cost $a_i$, and binary digit $b_i$ is written in it. He wants to have binary digit $c_i$ written in the $i$-th node in the end.

To achieve this, he can perform the following operation any number of times:

• Select any $k$ nodes from the subtree of any node $u$, and shuffle the digits in these nodes as he wishes, incurring a cost of $k\cdot a_u$. Here, he can choose $k$ ranging from $1$ to the size of the subtree of $u$.

He wants to perform the operations in such a way that every node finally has the digit corresponding to its target.

Help him find the minimum total cost he needs to spend so that after all the operations, every node $u$ has digit $c_u$ written in it, or determine that it is impossible.

Input

First line contains a single integer $n$ $(1\le n\le 2\cdot 10^5)$ denoting the number of nodes in the tree.

$i$-th line of the next $n$ lines contains 3 space-separated integers $a_i$, $b_i$, $c_i$ $(1\le a_i\le 10^9,0\le b_i,c_i\le1)$ — the cost of the $i$-th node, its initial digit and its goal digit.

Each of the next n−1 lines contain two integers $u$, $v$ $(1\le u,v\le n, u\ne v)$, meaning that there is an edge between nodes $u$ and $v$ in the tree.

Output

Print the minimum total cost to make every node reach its target digit, and −1 if it is impossible.

Examples

input

5
1 0 1
20 1 0
300 0 1
4000 0 0
50000 1 0
1 2
2 3
2 4
1 5

output

4

input

5
10000 0 1
2000 1 0
300 0 1
40 0 0
1 1 0
1 2
2 3
2 4
1 5

output

24000

input

2
109 0 1
205 0 1
1 2

output

-1

Note

The tree corresponding to samples $1$ and $2$ are:

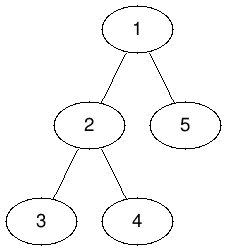
In sample $1$, we can choose node $1$ and $k=4$ for a cost of $4\cdot1 = 4$ and select nodes $1,2,3,5$, shuffle their digits and get the desired digits in every node.

In sample $2$, we can choose node $1$ and $k=2$ for a cost of $10000\cdot2$, select nodes $1,5$ and exchange their digits, and similarly, choose node $2$ and $k=2$ for a cost of $2000\cdot2$, select nodes $2,3$ and exchange their digits to get the desired digits in every node.

In sample $3$, it is impossible to get the desired digits, because there is no node with digit $1$ initially.

题意

有一颗树，树根为节点1，每个节点有三个属性$a,b,c$，$b$代表当前节点的状态，$c$代表当前节点需要变成的状态，$a$代表修改节点状态所需要的花费。

现在能够进行一种操作：

选择一颗以$u$为根节点的子树，任意的修改其子树中的$k$个节点的状态（互相交换），这个操作的花费为$k \cdot a_u$。

现在需要求解使树中所有节点都能变成目标状态所需要的最小开销，如果不存在则进行判定。

思路

首先可以知道，如果一个节点$i$的父亲节点为$p$，且有$a[i]>a[p]$，那么所有以$i$节点为根的子树上涉及到的操作都可以移动到其父节点上进行，可以对整棵树进行$a[i] = \min(a[i],a[p])$的操作而不改变本身的结果。

完成以上操作之后，根节点到叶子结点的值实际上就是一个单调递减的序列，可以从叶子结点往根节点进行遍历，一旦当前子树上存在可以操作的成对节点就进行操作。

时间复杂度为遍历树的时间复杂度$O(N)$。

代码

#include <bits/stdc++.h>
using namespace std;

#define maxn 200010
#define ll long long

int n;
ll a[maxn], b[maxn], c[maxn];
vector<int> g[maxn];
ll ans;

pair<ll, ll> solve(int u, int pa=0){
    a[u] = min(a[u], a[pa]);
    ll cnt0 = 0;
    ll cnt1 = 0;
    if(b[u] == 0 && c[u] == 1){
        ++cnt0;
    }
    else if(b[u] == 1 && c[u] == 0){
        ++cnt1;
    }

    for(auto v: g[u]){
        if(v != pa){
            auto tmp = solve(v, u);
            cnt0 += tmp.first;
            cnt1 += tmp.second;
        }
    }

    ll change = min(cnt0, cnt1);
    ans += change * a[u] * 2;
    return make_pair(cnt0-change, cnt1-change);
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin>>n;
    for(int i=1;i<=n;++i){
        cin>>a[i]>>b[i]>>c[i];
    }

    for(int i=1;i<n;++i){
        int u,v;
        cin>>u>>v;
        g[v].push_back(u);
        g[u].push_back(v);
    }

    a[0] = a[1];

    auto res = solve(1);

    if(res.first != 0 || res.second != 0){
        cout<<-1<<endl;
    }
    else{
        cout<<ans<<endl;
    }
}