[论文笔记] Bag of Tricks for Image Classification with Convolutional Neural Networks

往常的论文对于训练过程中的方法使用并不是非常关注，通常只能从代码中去寻找训练过程所采用的trick。

这篇文章介绍了一些训练图像分类CNN网络的trick，使用这些方法可以显著的提高分类网络的准确性。同时更好的准确性在迁移到object detection和semantic segmentation等任务上也会有更好的效果。

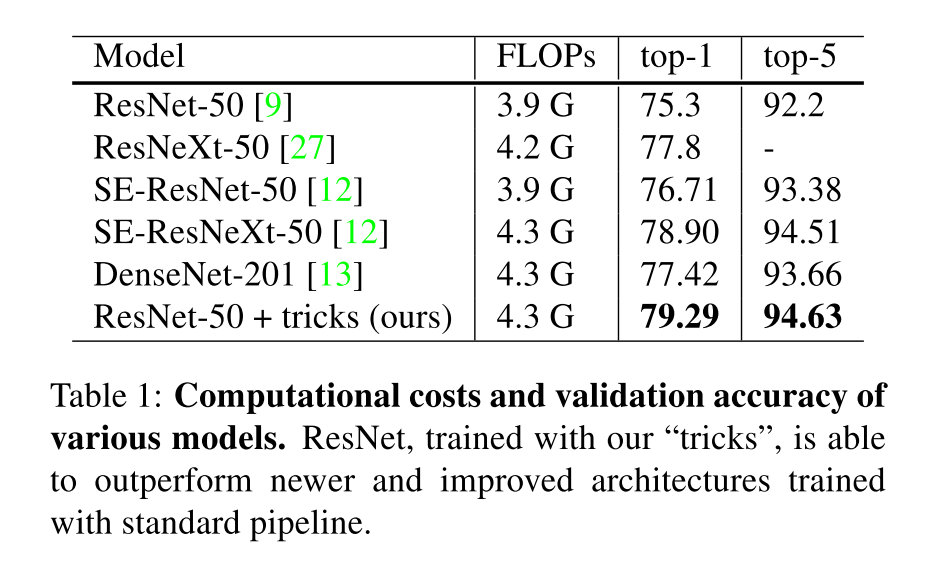
Training Procedures

利用随机梯度下降的方法来训练神经网络的基本流程如下所示，首先先对于baseline情况的超参数进行一个假定，之后再讨论优化的方法：

Efficient Training

使用更低的精度和更大的batch size可以使得训练更加高效，这里提供了一系列这样的方法，有的可以同时提升准确率和训练速度。

Large-batch training

使用更大的batch size可能会减慢训练进程。对于凸优化问题，随着batch size的上升，收敛速率会下降，在神经网络当中也有相同的情况。在同样数目的epoch情况下，用大的batch训练的模型在验证集上的效果会更差。

下面有四个启发式的方法用来解决上面提到的问题：

Linear scaling learning rate

理论上来说，从估计梯度的角度，提升batch size并不会使得得到梯度的大小期望改变，而是使得它的方差更小。所以可以对于学习率进行成比率的缩放，能够使得效果提升。

比如在当batch size为256的时候，选用0.1的学习率。

那么当采用一个更大的batch size，例如 $b$ 的时候，就将学习率设置为 $0.1\times b/256$ 。

Learning rate warmup

在训练开始的时候，所有参数都是随机设置的，离最终结果可能会非常远，所以采用一个较大的学习率会导致数值上的不稳定，所以可以考虑在最开始使用一个很小的学习率，再慢慢地在训练较为稳定的时候切换到初始学习率。

例如，如果我们采用前 $m$ 个batch来进行warm up的话，并且学习率的初值为 $\eta$ ，那么在第 $i$ 个batch， $1\le i \le m$ ，就选用大小为 $i\eta/m$ 的学习率。

Zero $\gamma$

ResNet是有很多个residual block堆叠出来的，每个residual block的结果可以看成是 $x+block(x)$ ，而block的最后一层通常是BN层，他会首先进行一个standardize，得到 $\hat{x}$ ，然后在进行一个缩放 $\gamma \hat{x}+\beta$ ，其中 $\gamma$ 和 $\beta$ 都是可学习的参数，通常被初始化为1和0。

可以考虑在初始化的时候，将所有的参数 $\gamma$ 都设置成0，这样网络的输出就和他的输入相同，这样可以缩小网络，使得在最开始的时候训练变得更简单。

No bias decay

weight decay通常被用于所有可学习的参数来防止正则化，这里的trick就是只作用于权重，而不对bias包括BN层当中的 $\gamma$ 和 $\beta$ 做decay。

Low-precision training

通常是采用FP32来进行训练的，但是大量的TPU在FP16上面的效率会高很多，所以可以考虑采用FP16来进行训练，能够达到几倍的加速。

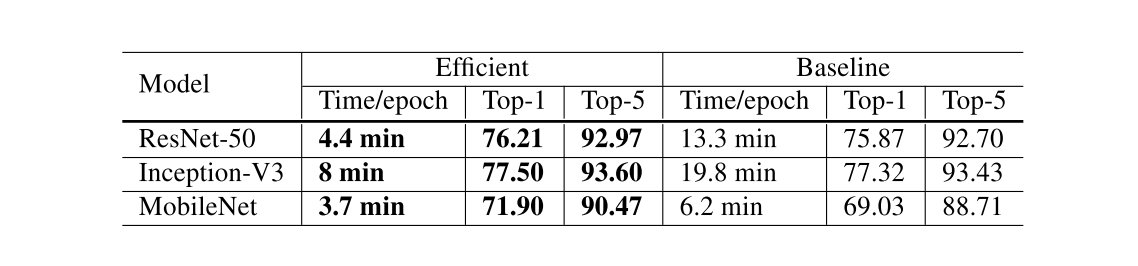
实验结果如上，其中Baseline的设置为 $BS=256$ ，采用FP32，Efficient的设置为 $BS=1024$ ，采用FP16。

Model Tweaks

原本的ResNet网络结构如图所示：

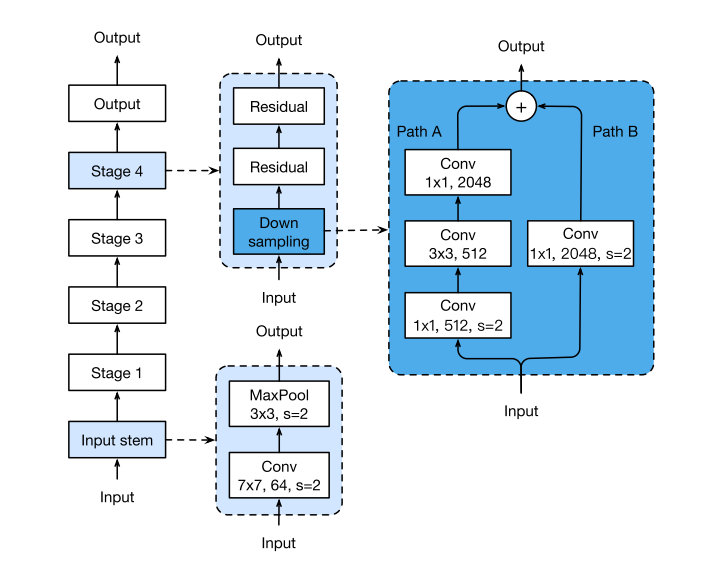
这里不多做介绍，文章提出了三种针对ResNet修改方式，分别记作ResNet-B/C/D，能够得到一定程度上的准确率提升。

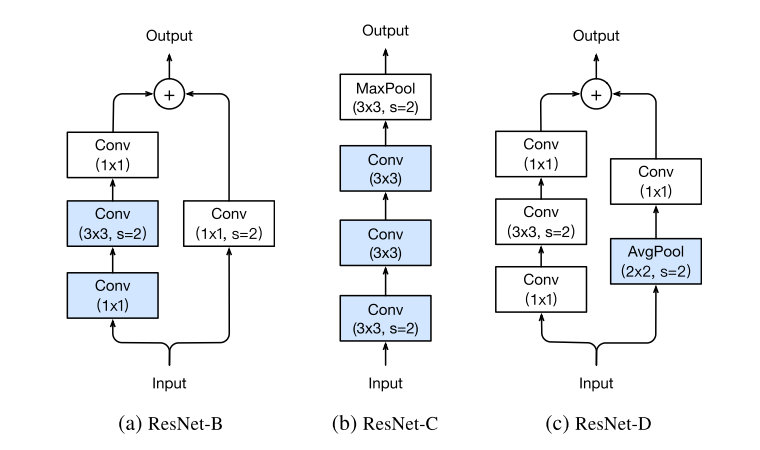
ResNet-B

第一个所做的就是改变了downsampling的方式，由于如果采用 $1\times 1$ 卷积同时选择stride为2的话，会丢失 $3/4$ 的信息，这里在 $3\times 3$ 的的卷积层来downsampling，理论上所有信息都会被接受到。

ResNet-C

一个发现就是卷积计算量随卷积核大小变化是二次多项式级别的，所以利用三层 $3\times 3$ 的卷积来替代 $7\times 7$ 的卷积层。

ResNet-D

从ResNet-B的角度更进一步，旁路也同样会有信息丢失的问题，所以将一层的 $1 \times 1$ 卷积修改成一层Average Pooling再加上一层卷积，减少信息的丢失。

Experiment Result

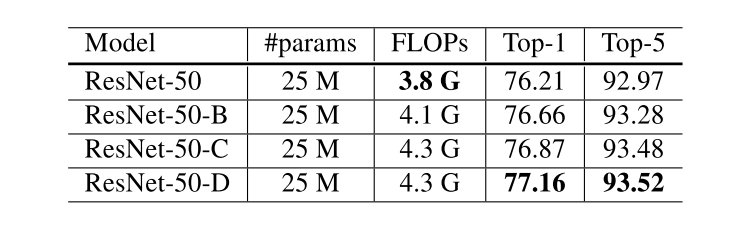
可以看到三者对于原始的ResNet结构准确率都有一定程度上的上升。

Cosine Learning Rate Decay

采用最广泛的策略是指数衰减。这里提供的一种方法是利用cosine函数进行衰减，忽略掉最开始进行warmup的部分，假设一共有 $T$ 个batch，那么在第 $t$ 个batch上，学习率为：

$\eta_t = \frac{1}{2}(1+\cos(\frac{t\pi}{T}))\eta$

其中 $\eta$ 就是初始的学习率，对比结果如下：

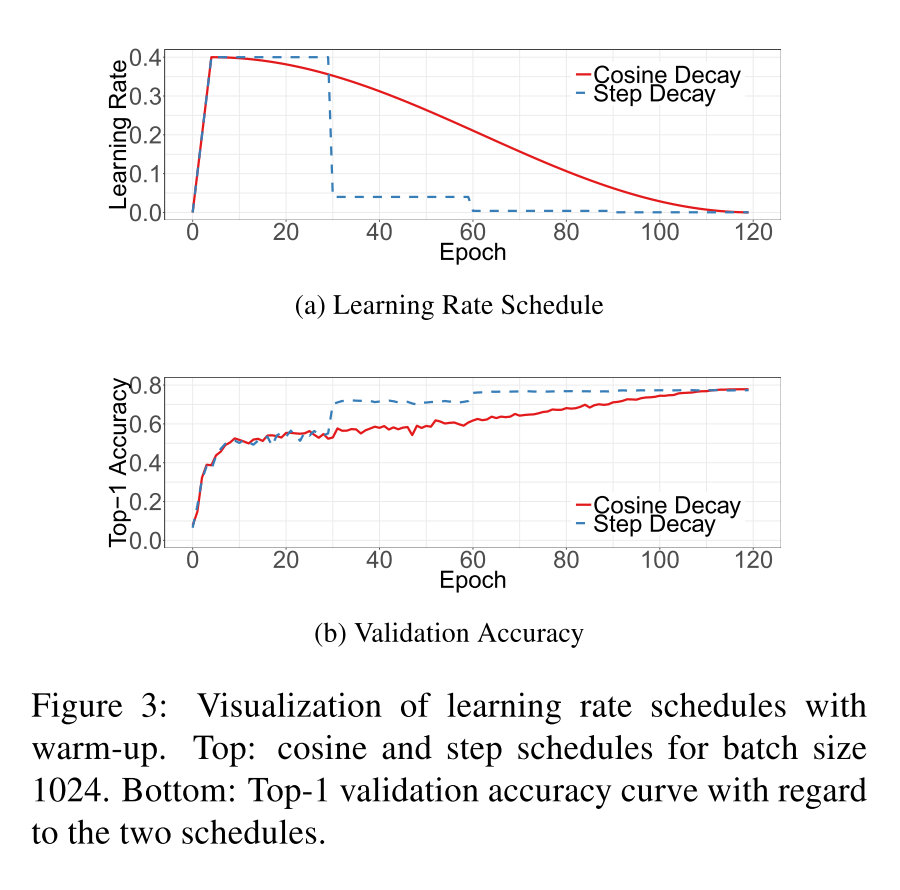
可以看到cosine decay在一开始和最终学习率下降的比较慢，在中间接近于线性的衰减。

Label Smoothing

对于分类任务，最后一层通常都是通过一个softmax函数来得到预测的概率，对于第 $i$ 类的结果 $q_i$ ：

$q_i = \frac{\exp(z_i)}{\sum_{j=1}^K \exp(z_j)}$

我们在学习过程当中最小化的是负的cross entropy：

$l(p,q) = -\sum_{i=1}^K p_i \log q_i$

$p_i$ 只有当 $i=y$ 的时候为1，其余时候为0，于是就等价于：

$l(p,q) = -\log(q_y) = -z_y + \log (\sum_{i=1}^K \exp(z_i))$

要达到最小化的效果应当有 $z_y^\star=\inf$ ，同时使得其他种类的 $z_i$ 尽可能小，换言之，这样会倾向于让预测结果趋于极端值，最终导致overfit。

label smoothing的思想就是将真实概率构造为：

$p_i = \begin{cases}1-\epsilon &i=y\\\epsilon / (K-1) & \text{otherwise}\end{cases}$

其中 $\epsilon$ 是一个小的常量，此时的最优解为：

$z_i^\star = \begin{cases}\log((K-1)(1-\epsilon)/\epsilon)+\alpha & i=y\\\alpha & \text{otherwise}\end{cases}$

其中 $\alpha$ 是一个实数，这会使得最终全连接层的输出会趋向于一个有限值，能够更好地泛化。

里面 $\log((K-1)(1-\epsilon)/\epsilon)$ 的部分就是正确分类和错误分类之间的gap，它随着 $\epsilon$ 的增大不断缩小，当 $\epsilon = (K-1)/K$ 的时候，实际上就是均匀分布，gap就为0了。

关于gap的可视化如下：

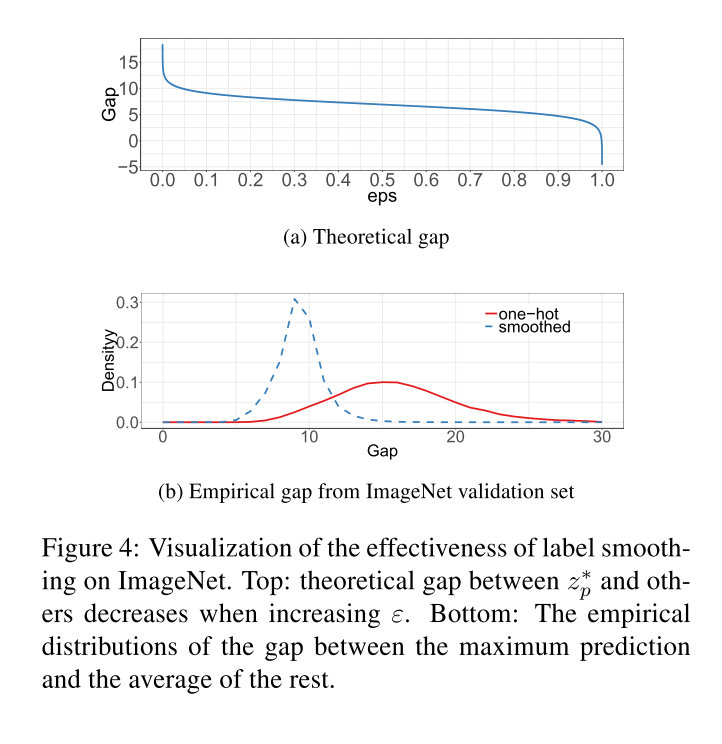
可以发现smooth之后gap总体均值变小，并且大gap的极端值情况有效减少了。

Knowledge Distillation

知识蒸馏中，我们尝试用一个学生模型来学习高准确率的老师模型里面的知识。方法就是利用一个distillation loss来惩罚学生模型偏离老师模型的预测概率。利用 $p$ 作为真实概率， $z$ 和 $r$ 分别作为学生网络和老师网络全连接层的输出，利用负的cross entropy作为loss，总的loss可以写成：

$l(p,\text{softmax}(z)) + T^2l(\text{softmax}(r/T),\text{softmax}(z/T))$

其中 $T$ 为温度超参数，使得softmax函数的输出变得更为平滑。

Mixup Training

作为一个数据增强的手段，每次随机选择两个样本 $(x_i,y_i)$ 和 $(x_j,y_j)$ 。然后对两个样本加权来作为新的样本：

$\begin{aligned} \hat{x} &= \lambda x_i + (1-\lambda)x_j \\ \hat{y} &= \lambda y_i + (1-\lambda)y_j \end{aligned}$

其中 $\lambda \in [0,1]$ 是一个从 $\text{Beta}(\alpha,\alpha)$ 中采样出来的数，在mixup中只对于新的样本 $(\hat{x},\hat{y})$ 来进行训练。