0%

Codeforces 1345D - Monopole Magnets

发表于

原文

A monopole magnet is a magnet that only has one pole, either north or south. They don’t actually exist since real magnets have two poles, but this is a programming contest problem, so we don’t care.

There is an n×mn\times m grid. Initially, you may place some north magnets and some south magnets into the cells. You are allowed to place as many magnets as you like, even multiple in the same cell.

An operation is performed as follows. Choose a north magnet and a south magnet to activate. If they are in the same row or the same column and they occupy different cells, then the north magnet moves one unit closer to the south magnet. Otherwise, if they occupy the same cell or do not share a row or column, then nothing changes. Note that the south magnets are immovable.

Each cell of the grid is colored black or white. Let’s consider ways to place magnets in the cells so that the following conditions are met.

  1. There is at least one south magnet in every row and every column.
  2. If a cell is colored black, then it is possible for a north magnet to occupy this cell after some sequence of operations from the initial placement.
  3. If a cell is colored white, then it is impossible for a north magnet to occupy this cell after some sequence of operations from the initial placement.

Determine if it is possible to place magnets such that these conditions are met. If it is possible, find the minimum number of north magnets required (there are no requirements on the number of south magnets).

Input

The first line contains two integers nn and mm (1≤n,m≤10001\le n,m\le 1000) — the number of rows and the number of columns, respectively.

The next nn lines describe the coloring. The ii-th of these lines contains a string of length mm, where the jj-th character denotes the color of the cell in row ii and column jj. The characters “#” and “.” represent black and white, respectively. It is guaranteed, that the string will not contain any other characters.

Output

Output a single integer, the minimum possible number of north magnets required.

If there is no placement of magnets that satisfies all conditions, print a single integer −1.

Examples

input

1
2
3
4
3 3
.#.
###
##.

output

1
1

input

1
2
3
4
5
4 2
##
.#
.#
##

output

1
-1

input

1
2
3
4
5
4 5
....#
####.
.###.
.#...

output

1
2

input

1
2
3
2 1
.
#

output

1
-1

input

1
2
3
4
3 5
.....
.....
.....

output

1
0

Note

In the first test, here is an example placement of magnets:

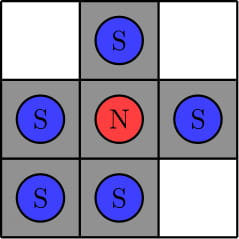
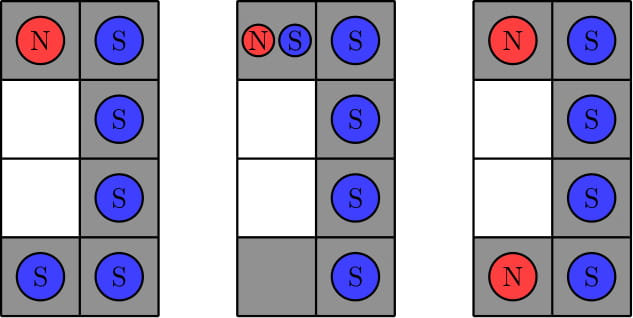
In the second test, we can show that no required placement of magnets exists. Here are three example placements that fail to meet the requirements. The first example violates rule 3 since we can move the north magnet down onto a white square. The second example violates rule 2 since we cannot move the north magnet to the bottom-left black square by any sequence of operations. The third example violates rule 1 since there is no south magnet in the first column.

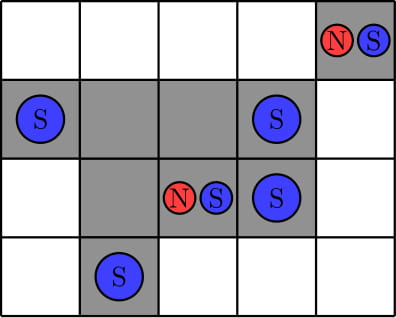
In the third test, here is an example placement of magnets. We can show that there is no required placement of magnets with fewer north magnets.

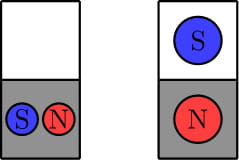
In the fourth test, we can show that no required placement of magnets exists. Here are two example placements that fail to meet the requirements. The first example violates rule 1 since there is no south magnet in the first row. The second example violates rules 1 and 3 since there is no south magnet in the second row and we can move the north magnet up one unit onto a white square.

In the fifth test, we can put the south magnet in each cell and no north magnets. Because there are no black cells, it will be a correct placement.

题意

有S和N两种磁铁，可以互相吸引，每次可以选择一个S和一个N激活，使得N向S方向移动，问需要有多少N磁铁可以满足（不限制S磁铁的数量）

  • 每一行列都存在S磁铁
  • 所有黑色区域都能够被N磁铁到达
  • 所有白色区域都不可能被N磁铁到达

如果无法满足以上三条规则，那么就输出-1。

思路

首先排除所有不可能满足的情况：

  1. 一行/一列有两段黑色区域，如果可以到达必定有S磁铁吸引，那么两段中间的白色区域就是可达的。所以每一行列必定只有一段黑色区域或全白。
  2. 全白行但是没有全白列（行列对换相同），如果存在的话，由于每一行需要有S磁铁，而S磁铁放置的列是有黑色区域的，如果N磁铁到达该黑色区域，然后激活空白行处的S磁铁，会导致白色区域可达。

综上，放置磁铁的方式为将S磁铁放置在所有黑色块中和空白行列相交处。

N磁铁需要每一个连通区域放置一个，由于N磁铁不能跨区域移动，所以这种放置方式是最优的。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include <bits/stdc++.h>
using namespace std;

#define ll long long
#define maxn 1010

char grid[maxn][maxn];
bool unused_row;
bool unused_col;
bool vis[maxn][maxn]; 
int dir[4][2] = {{-1,0},{1,0},{0,1},{0,-1}};
int n,m;

void bfs(int i, int j){
    queue<pair<int,int>> q;
    vis[i][j] = true;
    q.push(make_pair(i,j));
    while(!q.empty()){
        auto temp = q.front();
        i = temp.first;
        j = temp.second;
        q.pop();
        for(int k=0;k<4;++k){
            int ii = i + dir[k][0];
            int jj = j + dir[k][1];
            if(ii>=0 && jj>=0 && ii<n &&jj<m && grid[ii][jj] == '#' && !vis[ii][jj]){
                vis[ii][jj] = true;
                q.push(make_pair(ii,jj));
            }
        }
    }
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin>>n>>m;
    for(int i=0;i<n;++i)
        cin>>grid[i];

    for(int i=0;i<n;++i){
        int cnt = 0;
        if(grid[i][0] == '#')
            cnt = 1;
        for(int j=1;j<m;++j)
            if(grid[i][j] == '#' && grid[i][j-1] == '.')
                ++cnt;
        if(cnt > 1){
            cout<<"-1"<<endl;
            return 0;
        }
        if(cnt == 0){
            unused_row = true;
        }
    }

    for(int j=0;j<m;++j){
        int cnt = 0;
        if(grid[0][j] == '#')
            cnt = 1;
        for(int i=1;i<n;++i)
            if(grid[i][j] == '#' && grid[i-1][j] == '.')
                ++cnt;
        if(cnt > 1){
            cout<<"-1"<<endl;
            return 0;
        }
        if(cnt == 0)
            unused_col = true;
    }
  
    if(unused_row ^ unused_col){
        cout<<"-1"<<endl;
        return 0;
    }

    int cnt = 0;
    for(int i=0;i<n;++i){
        for(int j=0;j<m;++j){
            if(grid[i][j] == '#' && !vis[i][j]){
                ++cnt;
                bfs(i,j);
            }
        }
    }
    cout<<cnt<<endl;
}