量化笔试回忆版

某量化的机器学习岗笔试题，回忆如下，虽然我不知道这笔试和金融/机器学习有什么关系。考试时长四个小时，一共七道题，最后两道编程题选一题做就可以，所以平均下来是每题四十分钟。

一、最大回撤

题目背景：考虑一个股票的价格在 $N$ 天内的价格为 $P_1,P_2,\ldots,P_N$ ，一个投资者比较厌恶风险，他所能接受的最大回撤不能超过 $D$ ，试着计算他在这个最大回撤限制下的最大收益，算法复杂度需要是 $O(N)$ 的级别。最大回撤定义为 $\max(P_i-P_j),i<j$ ，其中 $i,j$ 都在买卖区间内。

我的解答：双指针+单调队列维护区间最大值

双指针靠左的指向买入日，靠右的指向卖出日，利用单调队列维护买卖区间中的最大值。每次当卖出日右移的时候检查是否满足最大回撤的约束，如果是就尝试更新最大收益，否则的话就左移买入指针，并尝试更新最大收益。卖出指针移动到末端的时候，仍然要依次左移买入指针直到末端，并尝试更新最大收益。由于两个指针都要遍历数组，容易知道复杂度是 $O(n)$ 的。

二、概率题——打乒乓球

题目背景：ABC三个人喜欢打乒乓球，但是一张球桌只能有两个人，所以有如下规则：每次两人对打，输家下场，换场下的人上场和赢家对打。那么三个人都非常好强，想要赢下另外两个人至少一局才算打爽了，（如A要打得爽，那么A需要赢过B也要赢过C），且只有所有人都打爽了球局才会结束，如果任意两个人的对局，都是五五开的，那么考虑以下两种情况：

如果第一局AB对阵，B胜利，第二轮BC对阵，C胜利，第三轮AC对阵，A胜利，第四轮AB对阵，A胜利。从这之后到所有人都打爽了，需要打的局数的期望是多少？
如果此时三个人刚刚来打球，那么要所有人都打爽了，需要打的局数的期望是多少？

我的解答：

考虑如下的状态转换：

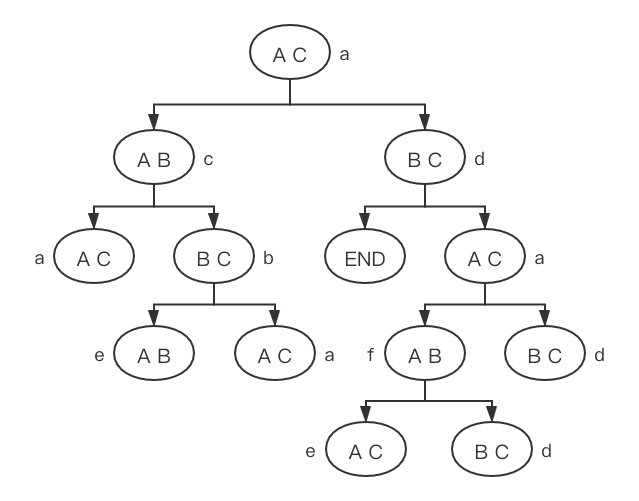
一共有一下六个状态 $abcdef$ ，他们对应状态要打的局数期望有以下关系：

$\begin{cases} a = 1 + (c+d)/2 \\ b = 1 + (a+e)/2 \\ c = 1 + (a+b)/2 \\ d = 1 + e/2 \\ e = 1+(d+f)/2 \\ f = 1 + (d+e)/2 \end{cases}$

可以解得：

$\begin{cases} a = 36/5 \\ b = 38/5 \\ c = 42/5 \\ d = 4 \\ e = 6 \\ f = 6 \end{cases}$

所以期望应当是 $36/5$ 轮次
我确实不会（菜狗哭泣），用它给的做编程题的窗口写了个代码跑模拟，得到的结果是 $62/5$ 的期望。

三、报数

题目背景：一共有2019个人依次编号，首尾相连占成一个圈，教练让从1号开始报数，依次报121212，每次报到2的人出局，由于是一个圈，所以可以一直循环下去。

问最后留下来的那个人的编号是多少？
小明拿到了1001号，但是他爸是教练，可以选择在任意时候给他爸一个眼神交流，让他爸讲报数顺序逆转，问小明有没有可能留到最后？

我的解答：

为了叙述方便首先定义轮次，从第1个人跑到最后算一个轮次，那么可以知道从第一轮留下来的都是奇数，相邻的人差的都是2，第二轮留下来的差的都是4，依次类推。所以容易发现每一轮留下来的人，在二进制表示上，有一位是相同的
2019的二进制表示为：

$111\ 1110\ 0011$

将其左移一位，末尾补1，找到在1~2019范围内的值就是所求的值，对应的二进制表示为

$111\ 1100\ 0111$

即留下来的是1991号。

有了前面的推断方法，我们可以判断在一共 $n$ 个人的队列中，处于第 $k$ 个的时候是不是最后留下来的，考虑1001的二进制表示为：

$011\ 1110\ 1001$

在倒数第二位的二进制表示出现不同，那么可以知道如果他爸不改顺序的话，他计划是在第二轮就被淘汰的。
这里进行讨论，首先看在第一轮的情况下，如果他爸在报数还没报到他的情况下就反转了，能不能让他留到最后。假设在他前面已经有 $n$ 个人出局了，那么就还剩下了 $2019-n$ 个人，由于在他之前，所以可以知道 $n<=500$ ，必定有 $2019-n>=1519>1024$ ，所以二进制表示保持有11位。
他爸有两种方法，一个是在第 $2n$ 号出局的时候，立刻反转由 $2n-1$ 号开始报1，他在队列中排 $1019+n$ 位，另一种是在 $2n+1$ 号报了1之后在进行反转，他在队列中排 $1019+n+1$ 位。
为了使得他能够留到最后，那么要满足以上情况：

$(2019-n-1024)*2+1 = 1019+n(+1)$

此处的 $(+1)$ 表示两种情况，整理可以得到：

$972= 3n(+1)$

可以发现，当不带 $(+1)$ 的时候， $n$ 是存在解的，即 $n=324$ ，所以在628号淘汰出局的时候，他爸立刻转向，让627号报1，小明就可以成为留到最后的人。

四、桥牌

问题背景：

一共除去大小王有52张牌，每人13张牌，大小次序为AKQJT98765432。
桥牌分为东南西北四家，其中南北为一队，东西为一队。按西北东南顺序出牌。
每一轮要根据第一轮出牌的花色来出牌，没有的话只能出其他花色的垫牌，垫牌必定小。这一轮最大的下一轮首先出牌。
西家先出牌，南北获胜的方法是赢下所有十三轮，东西获胜只要赢下一轮就可以。

问当四人都明牌的情况下，南北方的必胜策略是什么？

西家先出红心T

	西	北	东	南
黑桃	J876	A5432		KQT9
红心	[T]98	AKQ	7654	J32
方片	876	J2	T9543	AKQ
梅花	654	A32	T987	KQJ

西家先出红心T

	西	北	东	南
黑桃	76	AKQ5	JT98	432
红心	[T]987	KQJ	65	A432
方片	T98	5432	76	AKQJ
梅花	7654	A2	KJT98	Q3

西家先出红心6

	西	北	东	南
黑桃	J9876	A54	KT	Q32
红心	[6]5	432	KQJ987	AT
方片	7	AKQ6543	JT98	2
梅花	65432		T	AKQJ987

我的解答：真是绝了，这道题杀我，太久没打牌而陷入思维陷阱，笔试就只做出了第一个。

红心方片梅花北南都是绝对大，所以直接到下面这种情况，由于之前都是绝对大，此时北南可以控制由哪一边出牌

	西	北	东	南
黑桃	J8	A5		T9

此时南家出9，如果西家出J，北家出A大。如果西家出8，那么北家出5，让南家大。

南北两家出红心方片在可以绝对大八轮，在这中间北家垫牌梅花2，出梅花A大一轮，这个时候东家要垫四张牌，此时都是南家大。

	北	东（垫4张）	南
黑桃	AKQ5	JT98	432
梅花		KJT9	Q

如果东家垫的全部都是梅花，那么南家出梅花Q，北家垫掉黑桃5，之后北家三轮大。

如果东家垫过黑桃，那么北家黑桃AKQ5四轮都大。

第一轮打完东家出J逼南家出A大，之后北家有方片AKQ三张绝对大，之后难上手，一定会打掉梅花七张牌。由于西家黑桃J大不过北家的A和南家的Q，所以这里略去西家。

	北（垫7张）	东（垫6张）	南
黑桃	A54	KT	Q32
红心	43	KQ987	T
方片	AKQ6543	JT98	2

首先可以确定北家必定上手，那么东家不会留超过两张红心，红心789首先会被垫干净。

	北（垫7张）	东（垫3张）	南
黑桃	A54	KT	Q32
红心	43	KQ	T
方片	AKQ6543	JT98	2

之后北家角度来看，东家必然垫完了987之后，北家和南家都无法打过东家的牌，必然不会再打红心，所以北家的两张红心也会被垫干净

	北（垫5张）	东（垫3张）	南
黑桃	A54	KT	Q32
红心		KQ	T
方片	AKQ6543	JT98	2

那么北家不会再打红心，东家继续拿着两张红心是不合理的，但是南家还有一张红心，所以红心Q也会被垫掉

	北（垫5张）	东（垫2张）	南
黑桃	A54	KT	Q32
红心		K	T
方片	AKQ6543	JT98	2

这个时候，由于轮次的问题，北家必须要垫掉四张牌，然后才轮到东家决策，北家垫掉方片3456

	北（垫1张）	东（垫2张）	南
黑桃	A54	KT	Q32
红心		K	T
方片	AKQ	JT98	2

此时东家必定垫掉方片8，之后北家垫掉黑桃4

	北	东（垫1张）	南
黑桃	A5	KT	Q32
红心		K	T
方片	AKQ	JT9	2

东家肯定不会再动方片，那么最后一张垫牌就在红心K和黑桃T之间决策。

如果东家垫了黑桃T，那么南家走一张黑桃2，牌权交给北家，北家打完之后打掉方片三张，之后用一张黑桃5让南家黑桃Q大，游戏结束。

如果东家垫了红心K，那么南家走一张红心T可以大一轮，北家垫掉黑桃5，之后北家四张牌都是绝对大，游戏结束。

五、个人项目简答

就一个有关自己曾经做过项目的简答题，要求简明扼要，所占的分并不多。

六、算法编程——信封嵌套

问题背景：给定 $N$ 个信封，每个信封由两个数 $w,h$ 描述，表示信封的宽和高，如果一个信封的宽和高分别小于另外一个信封，那么就可以放入另一个信封，每个信封都可以进行90°的旋转，所以 $w,h$ 是可以互换的。

求出嵌套层数最多的方案。
如果不是信封而是三维盒子，求出嵌套最多的方案。

我的解答：在我的算法中，信封和盒子都没有任何区别，所以这里统一考虑。

容易写出针对于两个信封比较的函数，即一个信封能否装下另一个信封。对每两个信封都做一个对比，如果 $A$ 信封能够装下 $B$ 信封，那么建立一条 $A \rightarrow B$ 的连边。这样就构成了一个有向无环图，问题转变成了求图上的最长路径。

采用图上动态规划的方法来进行求解，每个节点上的val表示这个节点的信封作为最外层，所能够嵌套的层数，如果这个节点没有出边，那么将其val设置为1。否则的话，将他的val设置为子节点最大的val再加上1。遍历完整张图之后得到的最大的val值就是最大的嵌套层数。然后从有最大val值的节点进行一个DFS，就可以找到嵌套层数最多的方案。

建图的时间复杂度为 $O(N^2)$ ，进行遍历的时间复杂度为 $O(N)$ ，所以总的时间复杂度为 $O(n^2)$ 。可能有 $O(N\log N)$ 的解法？

Update：首先将两个数值进行排序，小的为高，大的为宽。之后对于一个排序，另一个利用树状数组进行维护，查看有多少高宽都小于它的信封就可以了，时间复杂度 $O(N\log N)$ 。

七、算法编程——螺旋数组

问题背景：给定一个边长为 $N$ ，数值由行列递增的方阵，问顺时针螺旋来读的话，第 $K$ 位数字是什么？要求算法能够在合理时间内求解 $N=30000000$ 量级的输入。

例如一个 $N=3$ 的方阵，数值就为：

$\begin{matrix}1&2&3\\4&5&6\\7&8&9\\\end{matrix}$

此时顺时针螺旋读的话，顺序就是 $1,2,3,6,9,8,7,4,5$ ，所以对于 $N=3,K=4$ 的情况得到的结果就是 $6$ 。

输入：两个整数 $N,K$

输出：一个整数

我的解答：首先确定对于 $K$ 个数，是属于第几个圈，之后确定第 $K$ 个数的行和列，然后计算得到结果。

时间复杂度为 $O(\log N)$ ，如果不考虑计算开方的复杂度可以认为是 $O(1)$ 的。

八、总结

笔试时长一共4个小时，除去高中竞赛之后好像基本没考过这么长的考试了。内容基本上全是智力测试，专业知识（金融知识）的考察基本为零，我觉得毫无准备硬冲基本非常容易一脸懵逼（对就是我）。不知道能不能过笔试（菜狗哭泣）。

Update

我这空了一道大题，编程算法题复杂度还写高了的居然过了笔试，不愧是我。