[论文笔记] Categorical Reparameterization with Gumbel-Softmax

Gumbel-Softmax Distribution

考虑$z$是一个定类型的变量，对于每个类型有着概率$\pi_1,\pi_2,\ldots,\pi_k$。考虑到从这个概率分布中的采样可以用一个onehot向量来表示，当数据量很大的时候满足：

$\mathbb{E}_p[z]=[\pi_1,\ldots,\pi_k]$

Gumbel-Max trick 提供了一个简单且高效的来对符合$\pi$这样概率分布的$z$进行采样的方法：

$z = \text{onehot} \left(\arg \max_i [g_i+\log \pi_i]\right)$

其中$g_i$是从Gumbel(0,1)中独立采出的，它可以利用Uniform(0,1)中的采样来计算得到：

$\begin{aligned} u &\sim \text{Uniform}(0,1) \\ g &= -\log(-\log(u)). \end{aligned}$

之后利用softmax来获得一个连续可导对argmax的估计

$\begin{aligned} y_{i}=\frac {\exp \left(\left(\log \left(\pi_{i}\right)+g_{i}\right) / \tau\right)} {\sum_{j=1}^{k} \exp \left(\left(\log \left(\pi_{j}\right)+g_{j}\right) / \tau\right)}\quad \text{for} \ i=1, \ldots, k \end{aligned}$

Gumbel-Softmax分布的概率密度如下表是：

$p_{\pi, \tau}\left(y_{1}, \ldots, y_{k}\right)=\Gamma(k) \tau^{k-1}\left(\sum_{i=1}^{k} \pi_{i} / y_{i}^{\tau}\right)^{-k} \prod_{i=1}^{k}\left(\pi_{i} / y_{i}^{\tau+1}\right)$

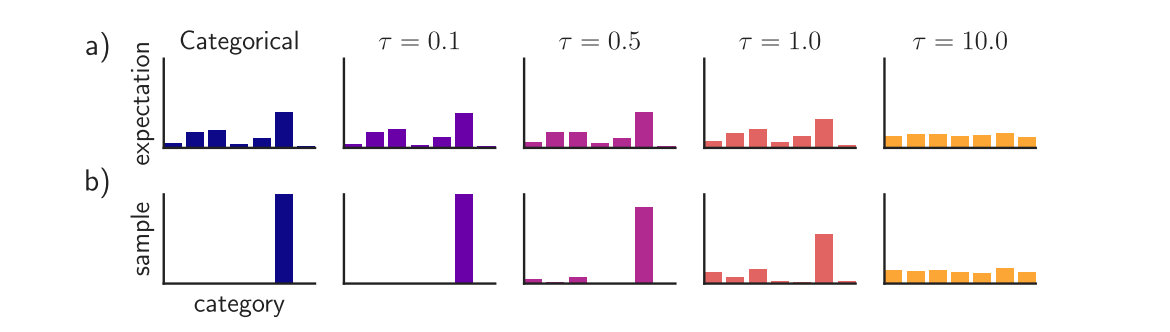
可以知道对于温度$\tau$而言，越接近于零，那么从Gumbel-Softmax分布中的采样就越接近onehot并且Gumbel-Softmax分布同原始的分布$p(z)$也更加的相似。

Gumbel-Softmax Estimator

可以发现对于任意的$\tau>0$，Gumbel-Softmax分布都是光滑的，可以求出偏导数$\partial y / \partial \pi$对参数$\pi$。于是用Gumbel-Softmax采样来代替原有的分类采样，就可以利用反向传播来计算梯度了。

对于学习过程中来说，实际上存在一个tradeoff。当$\tau$较小的时候，得到的sample比较接近onehot但是梯度的方差很大，当$\tau$较大的时候，梯度的方差比较小但是得到的sample更平滑。在实际的操作中，我们通常从一个较高的$\tau$开始，然后逐渐退火到一个很小的$\tau$。事实上，对于很多种的退火方法，结果都表现的不错。

Straight-Through Gumbel-Softmax Estimator

对于有些任务需要严格的将其限制为得到的就是离散的值，那么这个时候可以考虑对于$y$来做一个arg max得到$z$，在反向传播的时候利用$\nabla_\theta z \approx \nabla_\theta y$来进行梯度的估计。

即通过离散的方式进行采样，但是从连续的路径进行求导。这个叫做ST Gumbel-Softmax estimator，可以知道，当温度$\tau$较高的时候，这依然可以采样得到离散的采样值。

Related Work

主要总结了一些随机神经网络训练的方法，进行了一个对比。

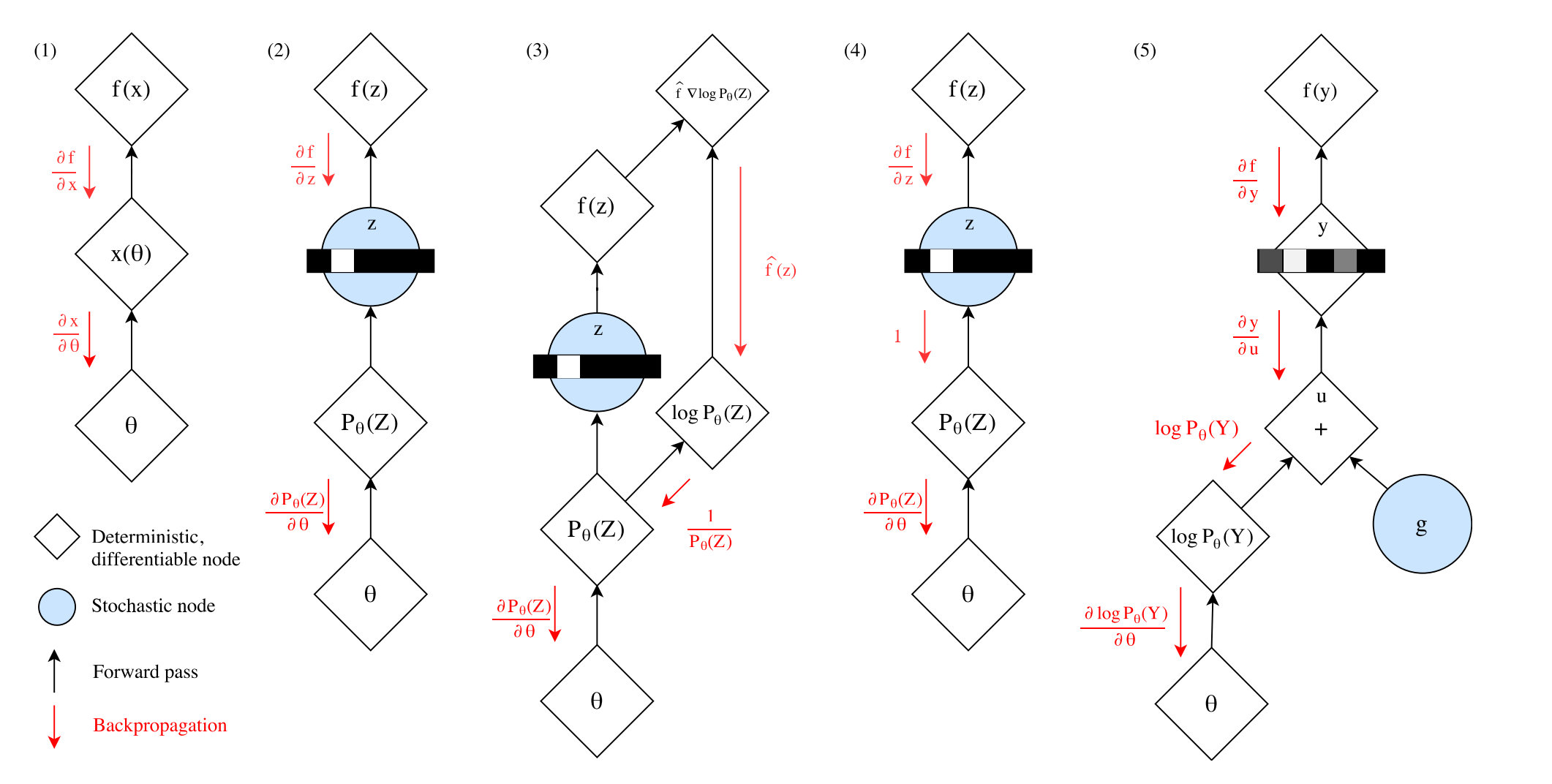
上图中

1. 正常的无随机节点的梯度下降
2. 存在随机节点的时候，梯度在这个地方不能很好地进行反传
3. 采用log trick绕开随机节点传递梯度
4. 估计梯度进行传播，例如前文提到的ST Estimator
5. 采用重参数化方法，就是这里的Gumbel-Softmax Estimator

Semi-Supervised Generative Models

对于重参数化和log trick就不再多说，这里看一个半监督生成模型的推断。

考虑到一个半监督网络，从带标签数据$(x,y)\sim\mathcal{D}_L$和不带标签数据$x\sim \mathcal{D}_U$中进行学习。

有一个分辨网络（D）$q_\phi(y|x)$，一个推断网络（I）$q_\phi(z|x,y)$，和一个生成网络（G）$p_\theta(x|y,z)$，通过最大化生成网络输出的log似然的变分下界来进训练。

对于带标签的数据，y是观测到的结果，所以变分下界如下：

$\begin{aligned} \log p_\theta(x,y) &\ge \mathcal{L}(x,y)\\ &= \mathbb{E}_{z \sim q_\phi(z|x,y)}[\log p_\theta(x|y,z)] - KL[q_\phi(z|x,y)||p_\theta(y)p(z)] \end{aligned}$

对于无标签数据，重点在于对于离散的分布没有办法进行重参数化，所以这里采用的方法是对于margin out所有类别的y，同样是在$q_\phi(z|x,y)$上面进行推断，得到的变分下界如下所示（有一说一我推的和论文不一样，但我觉得论文里面的公式写错了）：

$\begin{aligned}\log p_{\theta}(x) &\geq\mathcal{U}(x) \\&=\mathbb{E}_{z \sim q_{\phi}(y, z | x)}\left[\log p_{\theta}(x | y, z)+\log p_{\theta}(y)+\log p(z)-\log q_{\phi}(y, z | x)\right] \\&=\mathbb{E}_{z \sim q_{\phi}(y, z | x)}\left[\log p_{\theta}(x | y, z)-\log \frac{q_\phi(z|x,y)}{p_{\theta}(y) p(z)} + \log \frac{q_\phi(z|x,y)}{q_\phi(y,z|x)}\right]\\&=\mathbb{E}_{z \sim q_{\phi}(y, z | x)}\left[\log p_{\theta}(x | y, z)-\log \frac{q_\phi(z|x,y)}{p_{\theta}(y) p(z)} + \log \frac{1}{q_\phi(y|x)}\right]\\&=\sum_{y} q_\phi(y|x)\mathbb{E}_{z \sim q_{\phi}(z | x,y)}\left[\log p_{\theta}(x | y, z)-\log \frac{q_\phi(z|x,y)}{p_{\theta}(y) p(z)} + \log \frac{1}{q_\phi(y|x)}\right]\\&=\sum_{y} q_\phi(y|x)\mathbb{E}_{z \sim q_{\phi}(z | x,y)}\left[\log p_{\theta}(x | y, z)-\log \frac{q_\phi(z|x,y)}{p_{\theta}(y) p(z)}\right] + \sum_{y} q_\phi(y|x)\log \frac{1}{q_\phi(y|x)}\\&=\sum_{y} q_{\phi}(y | x)\mathcal{L}(x, y)+\mathcal{H}\left(q_{\phi}(y | x)\right)\end{aligned}$

最终得到的最大化目标为下面这个式子：

$\mathcal{J}=\mathbb{E}_{(x, y) \sim \mathcal{D}_{L}}[\mathcal{L}(x, y)]+\mathbb{E}_{x \sim \mathcal{D}_{U}}[\mathcal{U}(x)]+\alpha \cdot \mathbb{E}_{(x, y) \sim \mathcal{D}_{L}}\left[\log q_{\phi}(y | x)\right]$

容易发现，前两项一个是针对带标签数据的变分下界最大化，一个是针对无标签数据的最大化，最后一项代表分辨网络的对数似然，其中$\alpha$参数越大，说明越看重分辨网络的能力。是一个在分辨网络和生成网络之间进行tradeoff的参数。

对于这种方法，假设要margin out一共k个类别，那么对每个前向/反向步需要$\mathcal{O}(D+k(I+G))$，但是采用Gumbel-Softmax方法进行重参数化，就可以直接进行反向传播而不需要margin out，时间复杂度降低到了$\mathcal{O}(D+I+G)$，在类别很多的情况下可以有效降低训练的时间复杂度！