0%

[读书笔记] Deep Learning with Pytorch -- Chapter 4

发表于

开普勒从数据中得到三定律，同样利用的是现在数据科学的思想，他的步骤如下：

  1. 得到数据
  2. 可视化数据
  3. 选择最简单的可能模型来拟合数据
  4. 将数据分成两部分，一部分用来推导，另一部分用来检验
  5. 从一个奇怪的初始值除法逐渐迭代
  6. 在独立的验证集上检验所得到的模型
  7. 尝试对模型进行解释

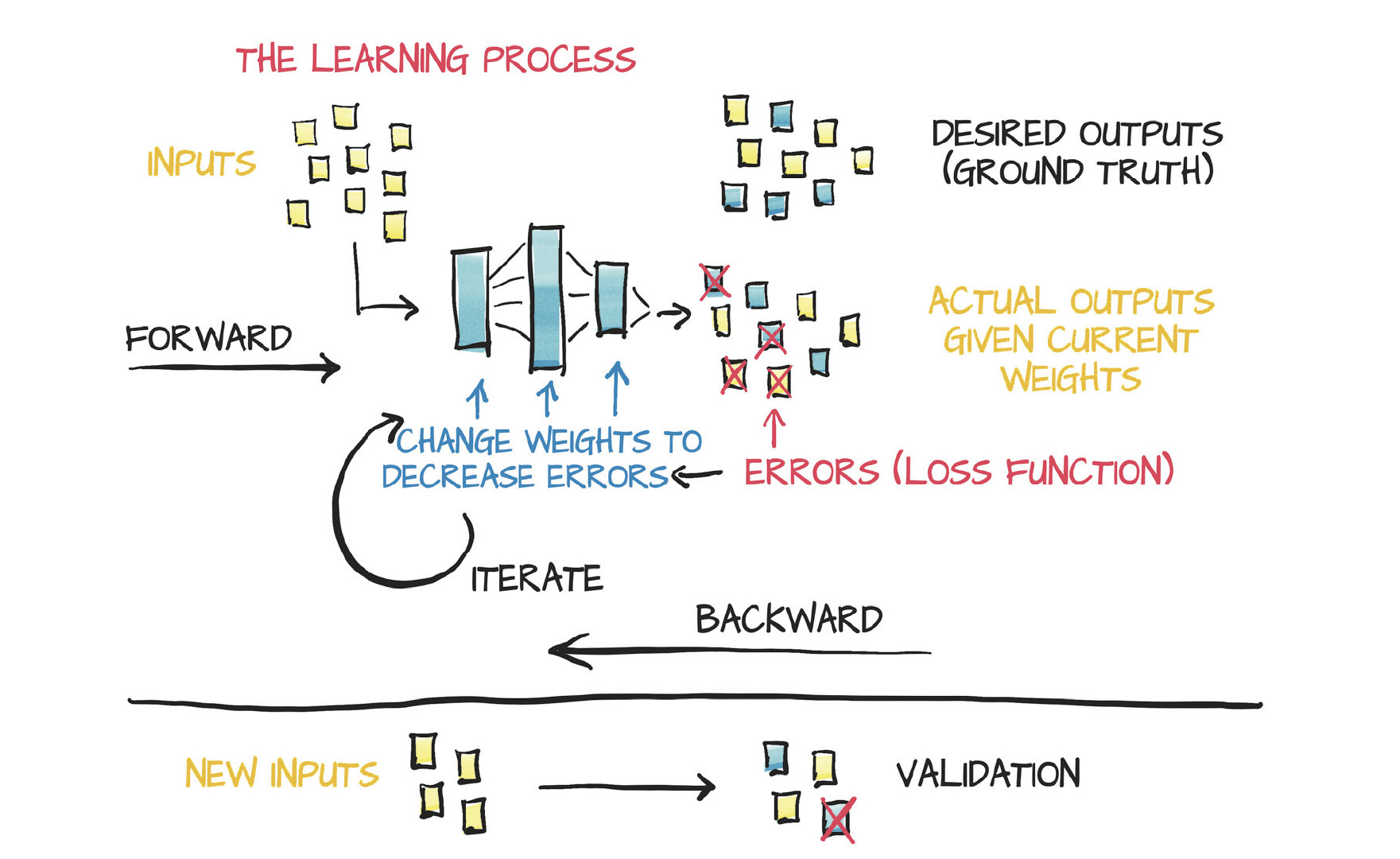
今日的学习方法实际上就是自动寻找适合的函数形式来拟合输入输出，流程如下：

输入测试数据->计算输出->计算误差->反向传播->更新权重

问题示例

一个简单的摄氏度和华氏度转换的方法。

定义model和loss函数：

1
2
3
4
5
6
def model(t_u, w, b):
  return w * t_u + b

def loss_fn(t_p, t_c):
  squared_diffs = (t_p - t_c)**2
  return squared_diffs.mean()

正向过程：

1
2
3
4
5
6
w = torch.ones(1)
b = torch.zeros(1)

t_p = model(t_u, w, b)

loss = loss_fn(t_p, t_c)

采用梯度下降进行反向传播，这里采用最简单的方法进行梯度的模拟计算：

1
2
3
4
5
6
7
8
9
delta = 0.1
learning_rate = 1e-2

loss_rate_of_change_w = (loss_fn(model(t_u, w+delta, b), t_c) - (loss_fn(model, t_u, w-delta, b), t_c)) / (2.0*delta)

loss_rate_of_change_b = (loss_fn(model(t_u, w, b+delta), t_c) - (loss_fn(model, t_u, w, b-delta), t_c)) / (2.0*delta)

w -= learning_rate * loss_rate_of_change_w
b -= learning_rate * loss_rate_of_change_b

上面这种方法会存在误差，可以考虑采用链式法则进行导数的计算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def loss_fn(t_p, t_c):
  squared_diffs = (t_p - t_c)**2
  return squared_diffs.mean()

def dloss_fn(t_p, t_c):
  dsq_diffs = 2 * (t_p - t_c)
  return dsq_diffs

def model(t_u, w, b):
  return w * t_u + b

def dmodel_dw(t_u, w, b):
  return t_u

def dmodel_db(t_u, w, b):
  return 1.0

def grad_fn(t_u, t_c, t_p, w, b):
  dloss_dw = dloss_fn(t_p, t_c) * dmodel_dw(t_u, w, b)
  dloss_db = dloss_fn(t_p, t_c) * dmodel_db(t_u, w, b)
  return torch.stack([dloss_dw.mean(), dloss_db.mean()])	# 利用stack合成一个tensor

对于一个训练轮次可以写成下面的样子：

1
2
3
4
5
6
7
8
9
10
11
12
def training_loop(n_epochs, learning_rate, params, t_u, t_c):
  for epoch in range(1, n_epochs+1):
    w, b = params
    
    t_p = model(t_u, w, b)
    loss = loss_fn(t_p, t_c)
    grad = grad_fn(t_u, t_c, t_p, w, b)
    
    params = parmas - learning_rate * grad
    
    print("Epoch %d, Loss %f" % (epoch, float(loss)))
  return params

对于不同的参数，可能得到的梯度大小会很不一样，一般将所有的输入做一个标准化的操作，从而能够使得训练更有效的收敛。

Autograd

autograd可以自动的根据运算求出导数，而不需要手动的对复杂的函数进行计算，考虑用autograd重写之前的内容：

1
2
3
4
5
6
7
8
def model(t_u, w, b):
  return w * t_u + b

def loss_fn(t_p, t_c):
  squared_diffs = (t_p - t_c)**2
  return squared_diffs.mean()

params = torch.tensor([1.0, 0.0], requires_grad = True)

requires_grad的效果是让pytorch在运算过程中对他的值进行追踪，每个参数都有.grad对象，正常情况下值为None。

1
2
loss = loss_fn(model(t_u, *params), t_c) # 加*相当于对参数进行解包，分别作为w,b传入
loss.backward()

通过backward()反传之后，params.grad不再是None。

多次运算，params上的梯度会被叠加，为了防止这样的事情出现，需要将梯度清零：

1
2
if params.grad is not None:
  params.grad.zero_()

现在训练过程长这个样子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def training_loop(n_epochs, learning_rate, params, t_u, t_c):
  for epoch in range(1, n_epochs + 1):
    if params.grad is not None:
      params.grad.zero_()
    
    t_p = model(t_u, *params)
    loss = loss_fn(t_p, t_c)
    loss.backward()
    
    params = (params - learning_rate * params.grad).detach().requires_grad_()
    
    if epoch % 500 == 0:
      print('Epoch %d, Loss %f' % (epoch, float(loss)))
  return params

detach将旧版本的参数从运算图中分离，requires_grad_使得参数可以被追踪导数。调用方法如下：

1
2
3
4
5
6
training_loop(
	n_epochs = 5000,
	learning_rate = 1e-2,
	params = torch.tensor([1.0,0.0], requires_grad = True),
	t_u = t_un,
	t_c = t_c)

Optimizer

可以通过下面的方法列出所有的优化器：

1
2
3
import torch.optim as optim

dir(optim)

每个优化器在构造的时候都针对一系列的参数(requires_grad = True)，每个参数都被存在优化器内部，使得可以通过访问grad来对他们进行更新。

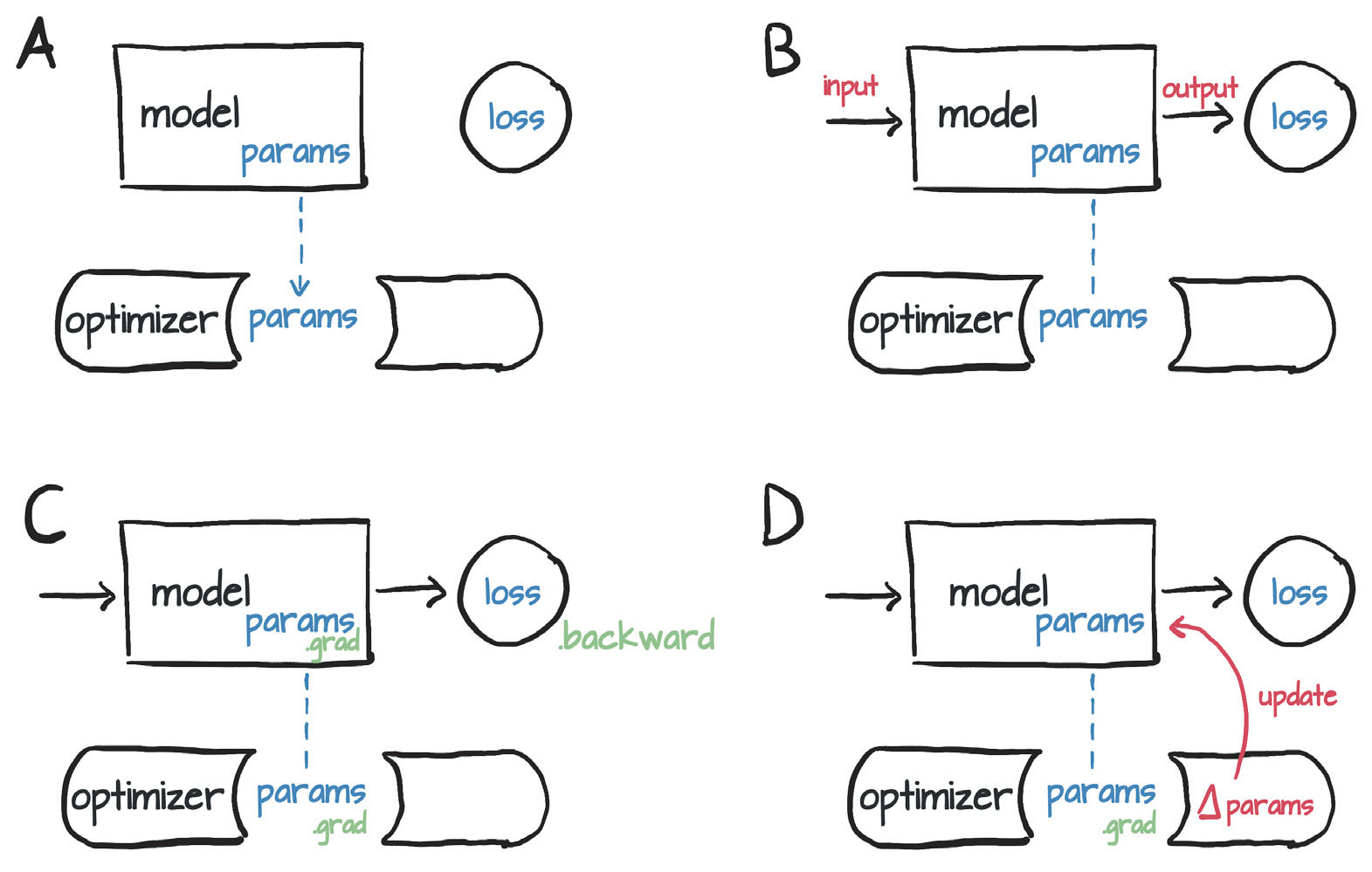
每个优化器都有两个方法：zero_grad和step，前者将所有在构建优化器时候传入的参数的grad全部设置成0，后者通过优化器自己的方法利用梯度对参数进行更新。

1
2
3
4
5
6
7
8
9
10
params = torch.tensor([1.0, 0.0], requires_grad = True)
learning_rate = 1e-5
optimizer = optim.SGD([params], lr = learning_rate)

t_p = model(t_un, * params)
loss = loss_fn(t_p, t_c)
# 正常的流程
optimizer.zero_grad()
loss.backward()
optimizer.step()

更改之后的训练流程：

1
2
3
4
5
6
7
8
9
10
11
12
13
def training_loop(n_epochs, optimizer, params, t_u, t_c):
  for epoch in range(1, nepochs + 1):
    t_p = model(t_u, *params)
    loss = loss_fn(t_p, t_c)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if epoch%500 == 0:
      print('Epoch %d, Loss %f' % (epoch, float(loss)))
      
  return params

训练集，验证集和过拟合

规则一：如果训练loss不下降，那么可能是模型太简单，或者是输入的信息不能很好地解释输出

规则二：如果验证集loss偏离，说明过拟合

缓解过拟合方法：

  1. 添加正则项
  2. 给输入加噪声生成新的数据
  3. 采用更简单的模型

可以考虑利用随机排序的下标来获得shuffle后的训练集和验证集：

1
2
3
4
5
6
7
n_samples = t_u.shape[0]
n_val = int(0.2*n_sample)

shuffled_indices = torch.randperm(n_samples)

train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]

由于并不会考虑在验证集的loss上反向传播，为验证集构造运算图是非常浪费内存和时间的事情，可以考虑利用torch.no_grad来提升效率：

1
2
3
4
5
6
7
8
9
10
11
12
13
def training_loop(n_epochs, optimizer, params, train_t_u, val_t_u, train_t_c, val_t_c):
  for epoch in range(1, n_epochs + 1):
    train_t_p = model(train_t_u, *params)
    train_loss = loss_fn(train_t_p, train_t_c)
    
    with torch.no_grad():
      val_t_p = model(val_t_u, *params)
      val_loss = loss_fn(val_t_p, val_t_c)
      assert val_loss.requires_grad == False  # 确认所有参数的requires_grad是False
      
    optimizer.zero_grad()
    train_loss.backward()
    optimizer.step()

或者可以使用set_grad_enabled来条件的启用反向传播

1
2
3
4
5
def calc_forward(t_u, t_c, is_train):
  with torch.set_grad_enabled(is_train):
    t_p = model(t_u, *params)
    loss = loss_fn(t_p, t_c)
  return loss